設σ是向量空間V上的兩線性形式,如果σ(x,y)=σ(y,x),x,y∈V,則稱σ為對稱雙線性形式。
基本介紹
- 中文名:對稱雙線性形式
- 外文名:the symmetric bilinear form
- 所屬學科 :數學(高等幾何)
- 相關概念:內積空間、雙線性形式等
定義

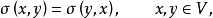
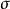
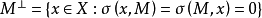
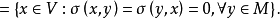
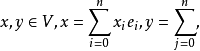

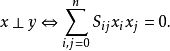
主要性質
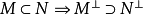
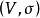
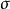

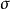
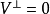
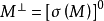
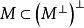
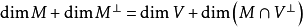
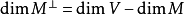
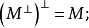
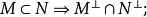
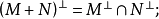

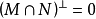
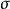
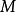
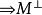

設σ是向量空間V上的兩線性形式,如果σ(x,y)=σ(y,x),x,y∈V,則稱σ為對稱雙線性形式。

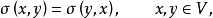
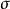
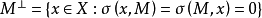
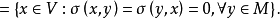
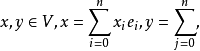

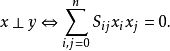
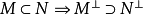
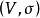
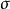

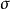
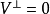
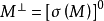
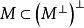
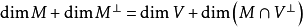
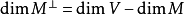
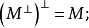
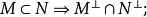
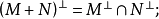

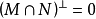
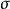
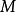
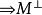
設σ是向量空間V上的兩線性形式,如果σ(x,y)=σ(y,x),x,y∈V,則稱σ為對稱雙線性形式。...
對稱雙線性型(symmetric bilinear form)是線性空間V上的雙線性型f(α,β),如滿足:對所有α,β∈V,都有f(α,β)=f(β,α),則稱f(α,β)為對稱雙線性...
如果V=W並且有B(v,w ) =B(w,v )對於所有V中的v,w,則我們稱B是對稱的。當這裡的X是F的時候,我們稱之為雙線性形式,它特別有用(參見例子標量積、...
數學中,一個辛矢量空間是帶有辛形式 ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
,習定義的分段光滑切向量場的集合,則指標形式I(·,·)是定義在.}<a,b)上的對稱雙線性形式方程式介紹其中X,YE.}Ca,b),X'(t)=Dr-X,Y'<t)=Dr.Y.若...
跡形式亦稱不變對稱雙線性形式,是線性空間中的雙線性函式的推廣。設A是域F上一個非結合代數, 是A上(作為線性空間)的一個雙線性形式,若還有 ,則稱這個雙線性...
在低層的域的特徵不是2的時候,二次形式等價於對稱雙線性形式。二次形式總是生成對稱雙線性形式(通過極化恆等式),而反過來要求除以2。...
上的二次形式,如果 對於所有 和 ,並且 是在 上的雙線性形式.這裡的 被稱為相伴雙線性形式;它是對稱雙線性形式。儘管這是非常一般性的定義,經常假定這個環 是...
拓撲4維流形弗里德曼定理(Freedman the-orem on topological 4-manifolds)是闡明4維流形的拓撲分類與相交形式之間關係的一個定理。根據關於對稱雙線性形式的分類與...
在雙線性代數中,正定矩陣的性質類似複數中的正實數。與正定矩陣相對應的線性運算元是對稱正定雙線性形式(復域中則對應埃爾米特正定雙線性形式)。...
因為每個正定形式都是非退化的,黎曼度量是偽黎曼度量的一個特殊例子。固此,可以把黎曼流形歸納為偽黎曼流形。每一個非退化對稱,雙線性形式有一個固定的度量符號 ...
嘉當-迪奧多內定理是數學中以埃利·嘉當與讓·迪厄多內命名的定理,此定理所涉及的是對稱雙線性形式的自同構群。...
在一個向量空間V中,定義在 上的正定對稱雙線性形式函式即是V的數量積,而添加有一個數量積的向量空間即是內積空間。點積代數定義 設二維空間內有兩個向量 和 ,...
對一般任何域上的有限維向量空間上的雙線性形式B,我們可對一組向量 定義一個格拉姆矩陣G為 。如果雙線性形式B對稱則該格拉姆矩陣對稱。...
在雙線性代數中,正定矩陣的性質類似複數中的正實數。與正定矩陣相對應的線性運算元是對稱正定雙線性形式(復域中則對應埃爾米特正定雙線性形式)。...
定義一個格拉姆矩陣 G為 。如果雙線性形式 B對稱則該格拉姆矩陣對稱。GRAM性質 編輯 1.半正定格拉姆矩陣是半正定的,反之每個半正定矩陣是某些向量的格拉姆矩陣。這...
非退化斜對稱雙線性形式和非退化“對稱”雙線性形式,比如歐幾里得向量空間的內積,的表現非常不同。歐幾里得內積 g,對任何非零向量 v,均有 g(v,v) > 0 成立;...
每一個非退化對稱,雙線性形式有一個固定的度量符號 (p,q)。這裡p 與q 記作正特徵值及負特徵值的個數。注意 p + q = n 是流形的維數。黎曼流形就是...
在微分幾何中,類似度量張量,里奇張量也是一個在黎曼流形每點的切空間上的對稱雙線性形式。以格雷戈里奧·里奇-庫爾巴斯托羅(Gregorio Ricci-Curbastro)為名的里奇...
數學中,一個辛向量空間是帶有辛形式ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
