基本介紹
- 中文名:奇異積分
- 外文名:singular integral
- 領域:數學
- 套用:諧波分析
- 定義:積分運算元
定義






卷積類型的奇異積分
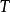


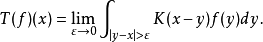

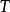



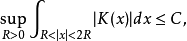


非卷積型的奇異積分
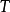
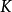

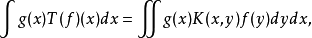






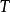


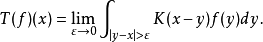

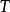

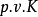


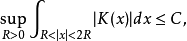


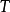
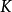

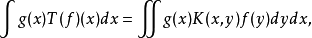
最重要的三類奇異積分方程是:1.柯西核的奇異積分方程(包括希爾伯特核的奇異積分方程),這是研究得最早和最完整的一類方程(其特點是未知函式出現在發散的積分號下,該積分只在柯西主值下有意義),以及和它的特徵方程有密切聯繫的黎曼...
奇異積分的交換子,調和分析中典型的一類非卷積運算元。設T1,T2是兩個運算元(一般說來,設它們的作用次序是不可交換的,即T1T2 T 2 T 1),定義 T 1與 T 2 的 交換子為 T 1 T 2- T 2 T 1,記為[ T 1, T 2],即...
振盪型奇異積分(oscillatory singular integral )是積分核中帶有振盪因子的一類奇異積分運算元。簡介 振盪型奇異積分是積分核中帶有振盪因子的一類奇異積分運算元。其定義為其中P(x,y)是Rⁿ×Rⁿ上的d階實多項式,K(x,y)為考爾德倫-...
《奇異積分交換子的有界性質》是依託北京師範大學,由陸善鎮擔任項目負責人的面上項目。項目摘要 奇異積分運算元的交換子作為Calderon-Zygmund理論中第二代非卷積型運算元,其有界性質的研究一直備受重視,其中,二十世紀九十年代中期的Alvarez等人...
《奇異積分運算元理論中若干問題的研究》是依託浙江大學,由陳杰誠擔任項目負責人的面上項目。項目摘要 本項目主要研究如下幾個問題:.1、帶齊次核的標準CZ奇異積分運算元的弱型L1-有界的Calderon猜測,即:當核函式的球面部分為LlogL函式時...
《奇異積分和相關論題》是2011年世界圖書出版公司出版的圖書,作者是陸善鎮。內容簡介 《奇異積分和相關論題》是一部為分析專業的研究生量身定做的入門書籍。《奇異積分和相關論題:英文(影印版)》是以歐幾里得空間為背景,清晰明確的闡釋了...
《一類奇異積分及位勢的分形邊界性質的研究》是依託武漢大學,由章逸平擔任項目負責人的面上項目。項目摘要 結合分形幾何、位勢理論、奇異積分等方法技巧,揭示具有分形邊界或分形支撐的位勢和解析函式的奇異邊界性質。以此為突破口,通過...
《奇異積分和函式的可微性》是 2011年 世界圖書出版公司出版的圖書,作者是(美國)施泰恩(SteinE.M.) 。內容簡介 《奇異積分和函式的可微性(英文)(影印版)》內容簡介:ThisbookisanoutgrowthofacoursewhichIgaveatOrsayduringtheacademic...
奇異積分的近似計算(numerical computationof singular integrals)計算奇異積分近似值的數值方法。在套用上常遇到計算奇異積分的問題{:,(x)f(x)dx,這裡右端第一個積分可逐項求出,而第二個積分的 被積函式已經相當光滑,可用求積公式算...
《振盪奇異積分運算元及變數核超奇異積分交換子》是依託北京科技大學,由陳艷萍擔任項目負責人的數學天元基金項目。項目摘要 首先,本項目要研究的第一個問題是卷積型振盪奇異積分運算元和沿曲面的奇異積分運算元當核屬於H^1(S^{n-1})時,在...
相聯方程(adjoint equation)在奇異積分方程理論中有著重要關係的一對方程的名稱。.奇異積分方程 互相稱為相聯的方程.這兩個方程中任一個是另一個將核k(t,r)/(r-t)中的t和:互換得出的.對應的運算元七久和七久‘互相稱為相聯運算元,...
諾特定理,是奇異積分方程的基本定理,為理論物理的中心結果之一,它表達了連續對稱性和守恆定律的一一對應。諾特定理對於所有基於作用量原理的物理定律是成立。它得名於20世紀初的數學家埃米·諾特。諾特定理和量子力學深刻相關,因為它僅用...
《復變邊界行為》是依託武漢大學,由杜金元擔任項目負責人的面上項目。項目摘要 本研究課題《復變邊界行為》涉及解析函式邊值問題和奇異積分方程方向上諸多的理論和套用。在本課題中,研究者們系統討論了各類廳異積分運算元的指標、準逆、零...
1、《Banach空間中一類積分—微分方程邊值問題的解》,《山東大學學報(理學版)》2002年第6期;2、《Banach空間中一類非線性積分—微分方程邊值問題的解》,《套用泛函分析學報》2003年第4期;3、《Banach空間中奇異積分-微分方程邊值...
在柯西型積分的表達式中,f(t)稱為它的核密度,1/t-z稱為柯西核。柯西核的奇異積分方程包括希爾伯特核的奇異積分方程,這是研究得最早和最完整的一類方程。柯西型積分 柯西型積分是柯西積分的推廣。下列積分稱為柯西型積分:其中L為...
韋夸等價正則化定理(Vekya equivalent regu-larization theorem)斷言奇異積分方程在一定意義下均可等價於某一弗雷德霍姆方程的定理.韋夸定理斷言:奇異積分方 .}} _ .f ( i)(在下面指出的意義下)一定等價於某個弗雷德霍姆方程.具體地...
《超高速切削主軸系統的關鍵技術研究》是依託同濟大學,由諸乃雄擔任項目負責人的面上項目。中文摘要 提出了高階奇異積分Hadamard主值的新定義,得到了Bochner-Martinelli型,復超球面積Clifford空間中的Cauchy型高階積分的Plemelj公式,高階...
廣義維納一霍普夫方程是數學中的一種方程。廣義維納一霍普夫方程(generalized Wiener-Hopf equation) IL類主要奇異積分方程的統一名稱.多年來人們企圖用統一觀點去處理已經分別研究得相當深人的幾類主要的奇異積分方程,即柯西核積分方程、...
特別是發展了奇異積分理論,奇異積分運算元後成為偽微分運算元的重要組成部分,它不僅深刻影響偏微分方程理論而且用於指標定理。卡爾德隆在1958年證明柯西問題的唯一性。1980年證明李普希茨曲線上的柯西積分的L2有界性,這蘊涵複分析的當儒瓦猜想。...
近幾十年來, 這類問題也獲得了眾多專家學者的極大關注. 本項目主要研究高振盪Bessel型積分、幾類高振盪奇異積分、多頻高振盪積分以及高維高振盪積分的計算、高振盪奇異積分方程的數值解以及圖像重建中遇到的高振盪問題, 為了克服奇異性和...
維納一霍普夫方程(Wiener-Hopf equation)是一種帶差核的奇異積分方程。古典的維納一霍普夫方程是指下述的帶差核的奇異積分方程 方程(1)的研究開始於20世紀20年代初,早期著名例子是輻射傳輸理論中的米爾恩方程,後因1931年由維納(Wiener...
里斯運算元是一類重要的高維奇異積分運算元,在雙曲型偏微分方程的理論中有重要套用。簡介 里斯運算元是一類重要的高維奇異積分運算元。它是指下面的m個運算元其中 是n維空間Rⁿ的點,性質 里斯運算元是將f∈L²映射到L²的有界運算元,對m=1,...
一種利用Fourier分析,主要藉助奇異積分的成熟理論。另一種辦法是局部化方法,主要利用橢圓或拋物型方程的技巧。..近年來分數階偏微分方程的研究在Hölder空間取得了很多重要的成果。由於分數階偏微分方程的複雜性,大量的問題仍然沒有解決...
