基本介紹
- 中文名:向量叢映射
- 外文名:vector bundle map
- 領域:數學
- 定義:向量叢之間的映射
- 性質:流形切叢概念的推廣
- 空間:底空間、全空間
概念

向量叢




向量叢是流形切叢概念的抽象和推廣,它是微分拓撲學和代數拓撲學的重要研究對象。映射亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係,G的定義域D(G)為X,且對任何x∈X都有惟一的y∈Y滿足G(x,y...
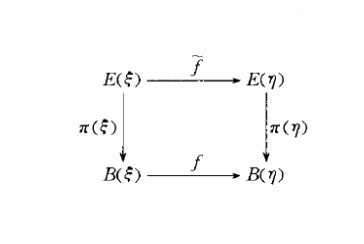
一個從向量叢π₁:E₁→X₁到向量叢π₂:E₂→X₂的態射(morphism)是一對連續映射f:E₁→E₂和g:X₁→X₂使得 gπ₁= π₂f 對於每個X₁中的x,由f誘導的映射π₁({x}) → π₂({g(x)})是一個向量空間的線性變換。所有向量叢的類和叢的射組成了一個範疇。限制到...
映射的第二基本形式(second fundamentalform of a map)由映射確定的重要微分形式.設M和N為黎曼流形,f:M->N為光滑映射.記f-`TN為f決定的M上的誘導向量叢。它的誘導聯絡記為守.於是,映射f的第二基本形式a(f)是向量叢T " M⑧T " M⑧.f-' TN的一個截面,定義如下:式中1-'`; I'a,.分別是...
巴拿赫向量叢是每點處的纖維均拓撲線性同構於某巴拿赫空間且局部平凡的叢。簡介 巴拿赫向量叢是每點處的纖維均拓撲線性同構於某巴拿赫空間且局部平凡的叢。一個叢指的是三元組ξ=(G,π,B),其中G和B是拓撲空間,π:G→B是連續滿映射。G和B分別稱為叢ξ的全空間與底空間,π稱為投影。對每點b∈B,π(b)...
誘導向量叢(induced vector bundle),亦稱向量叢的回退。由連續映射從一個向量叢按自然方式誘導產生的向量叢,這是構造新向量叢的常用方法之一。設:(E,p,B)為向量叢,.f : B' ->B為連續映射,記 成為一個向量叢,稱為誘導向量叢,記為.f' }.對於.f' }有典型的向量叢映射(了,.f>,其中因而是...
象徵映射(symbol map)是流形上復向量叢的擬微分運算元空間到對應的象徵空間的映射。簡介 象徵映射是流形上復向量叢的擬微分運算元空間到對應的象徵空間的映射。設X是C流形,E和F是X上的復向量叢,對於任意一個擬微分運算元P∈PDiffₖ(E,F),總存在一個線性映射 稱σₖ為象徵映射。性質 象徵映射σₖ有下述...
商向量叢(quotient vector bundle)一種常見的向量叢.它是由兩個同一底空間上的向量叢及其適合一定條件的叢同態構造的.設寧,7均為B上的向量叢,.f:E(護-E )為叢同態,在E 上定義等價關係“一”,於是當叢同態f.適合b .fn=.f 是單的線性映射時,(EB)是向量叢,稱為由f決定的寧的商叢,記為x.或...
向量叢限制 向量叢限制是一個數學術語。向量叢限制(restriction of vector bundle)一類特殊的向量叢.它是由一個已知的向量叢派生出來的.若(E,p,B)為向量叢,則B是向量叢,稱為在B上的限制,記為可看成包含映射i:B。決定的誘導向量叢.
它在研究向量叢的分類性質中起重要作用.設GCn,k)是R”中k (1 則向量叢稱為泛向量叢.對於向量叢,一個重要的定理是:若n)k+m,則對於任意m維微分流形M上的k維向量叢寧,都存在連續映射g;M->G(n,k),使得誘導向量叢 yn=k.這也是y稱為泛叢的原因.
向量叢同構是底空間相同的兩個向量叢之間一種特殊的向量叢等價。按此等價關係討論向量叢的同構分類是向量叢的重要問題之一設子,夕是B上兩個向量叢(即B-B),對於連續映射:(E> E),若交換,並且對於bEB,Eb是線性映射,則稱為向量叢子到夕的叢同態.進而,若對於(bEB,了Eb+)是同構,則了稱為向量叢同構,...
設ξ=π:E→B為B上兩個向量叢。則映射h:E₁→E₂稱為叢同態,若h將纖維E線性映射到E。等價地,h:E₁→E₂為同態叢Hom(ξ₁,ξ₂)的截面。簡介 叢同態是兩個向量空間之間保持纖維中代數結構的映射。η到ξ的叢同態是一個連續函式g把每個向量空間F(η)線性地映到向量空間F(ξ)之上,其中記號...
記為E⊕F。這兩個向量叢的直和,實際上就相當於對底空間的每一點上的纖維進行線性空間的直和。簡介 設x,y分別是n維,k維向量叢,都以B為底空間,其圖冊分別是Y設 作為圖冊,B是((n+k)維向量叢,稱為x與y的惠特尼和,記為By。而x也可看成積叢BX 由對角映射f;B>BXB決定的誘導叢。
纖維叢論是纖維叢(fibre bundle)向量叢的一般化和推廣。代數拓撲的重要研究對象。設E,B,F均為拓撲 空間,為連續映射,稱為纖維叢,若滿足:對於 ,都有b在B中的鄰域 及同胚映射 ,使得對於 此時 稱為叢射影,B稱為 的底空間,F稱為 的導空間(纖維),E稱為叢空間。當纖維叢 的導空間是向量空間 時...
從而法叢一般是周圍空間對限制在子叢上切叢的商。正式地,N在M中的法叢是M的切叢的一個商叢: 我們有N上向量叢的短正合序列:這裡 是M的切叢限制在N上(準確地說,M的切叢 通過映射 拉回到N上)。穩定法叢 抽象流形由一個典範切叢,但沒有法叢:只有當一個流形嵌入(或浸入)另一個流形時誘導了一個法...
聯絡映射是微分幾何的一個概念。定義 設𝓗為向量叢ξ=π:E→M的聯絡,則有τE=𝓥⨁𝓗。由於𝓥≅π*ξ,則有π₂:E(𝓥)=π*E→E。𝓗的聯絡映射κ:TE→E定義為 κ(w)=π₂(w),w∈TE。等價定義為 對ω∈TE,令p:=π(u),ι:Eₚ→E為包含映射。則E(𝓥)=ι(Eₚ)u={...
共軛叢(conjugate bundle)是與復向量叢相關且有相互復結構的向量叢。簡介 共軛叢是與復向量叢相關且有相互復結構的向量叢。若ω 是一個復向量叢,共軛叢 是一個復向量叢,與ω有相同的基本實向量叢 但有“相反的”復結構,因而映射 是共軛線性的,即對每個複數λ 及每個 ,有 其中 是 的共軛複數...
截面是纖維叢理論的一個概念。拓撲空間定義 設π:M→N為連續映射,則π的截面為π的連續右逆,即連續映射σ:N→M滿足π∘σ=Id。向量叢定義 設ξ=π:E→M為向量叢。則E的截面或整體截面為π的截面,即一個連續映射σ:M→E,滿足π∘σ=Id。故對M上一點p,σ(p)為纖維Eₚ的一個元。設ξ=π:...
斯蒂弗爾-惠特尼類(Stiefel-Whitney class)是一種相應於正交群O(n)的模2係數的示性類,它有很多基本性質,如:若ξ=η,則W(ξ)=W(η);若ε為平凡叢,則W(ε)=0,i>0,這是因為存在從ε到底空間為一個點的向量叢的映射;若ε為平凡叢,則W(ε⊕η)=W(η)。基本介紹 斯蒂弗爾-惠特尼類是一種...
分類空間是在纖維叢理論中起關鍵作用的一類空間。任意拓撲群 G 的分類空間總是存在的。分類空間的確切含義由分類定理得到體現。簡介 分類空間是在纖維叢理論中起關鍵作用的一類空間。分類空間是針對於拓撲群而言。定義 定義1 設ξ為B上n階向量叢,γ為格拉斯曼流形G上的n階萬有叢,當l足夠大時,存在映射f:B→G...
局部向量叢(乘積向量叢)上的聯絡 設U是微分流形上的一個坐標鄰域,局部坐標為x=(x1,x2,…,xn),F是一個m維實(或復)向量空間,稱為以U為底F為標準纖維的乘積叢。由於F是向量空間,U×F是一個乘積向量叢。為U×F到U的投影運算元。設有可微分映射σ:U→U×F使,就稱映射σ為一截面(也可稱為向量場)...
為底空間的向量叢ξ是很多的,當 為可微流形時,稱切叢 的斯蒂弗爾-惠特尼類為M的斯蒂弗爾-惠特尼類。對於流形M,若 為平凡叢,則稱M為可平行化的。設 為 個 的惠特尼和,其全空間中的每一個點可以表為 其中 是x在 中的像點,則存在一個叢映射 (ε′為一維平凡叢), 其中 為 的內...
自然性。若f:B→B'被一個保定向的叢映射f*ξ→ξ覆蓋,則e(f*ξ)=f*e(ξ)。若把ξ的定向反向,則歐拉類e(ξ)變號;若纖維維數n是奇數,則e(ξ)+e(ξ)=0;惠特尼和的歐拉類滿足e(ξ⨁ξ')=e(ξ)∪e(ξ')。類似地,笛卡兒積的歐拉類滿足 e(ξ×ξ')=e(ξ)×e(ξ')若定向向量叢ξ...
設M為實流形,ξ=π:E→M為復向量叢,為在E上取值的第i微分形式層。向量叢E上的聯絡為複線性層同態 ,且對任何M上的局部函式f與E上的截面s,滿足萊布尼茨公式 。構造 聯絡為底空間為M的向量叢之間的一個態射 ,滿足 ,且 為雙線性映射。兼容 每個向量叢都兼容聯絡。設 為ξ的垂直叢的總空間,為 在TE...
幾何直觀上說, 切叢就是流形上每一點處的切空間“粘合”在一起得到的新流形--即向量叢。這是流形自帶的一個向量叢,它反映了該流形的大範圍性質和局部性質的聯繫。性質 設ξ=π:E→B為向量叢,π:TE→TB,由於將u∈E的纖維線性滿映射到π(u)∈B的纖維上,則π誘導出滿態射h:TE→π*TB,則kerh=ker...
由包含映射 序列 ,可生成群同態序列 定義δ:為 則 為切赫鏈復形 。的上同調為切赫上同調 。設 為 的開加細,由限制映射得 ,這與j的選取無關。由歸納極限可得M上的切赫上同調為 性質 若ω∈ ,則 設K為單純復形,M為其底拓撲空間。則M上常數層 的切赫上同調同構於K的單純上同調,即 向量叢 構造 ...
