纖維叢論是纖維叢(fibre bundle)向量叢的一般化和推廣。代數拓撲的重要研究對象。
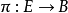




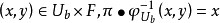
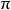





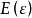


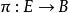
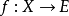

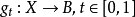
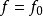

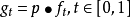
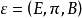
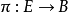
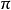

纖維叢論是纖維叢(fibre bundle)向量叢的一般化和推廣。代數拓撲的重要研究對象。
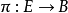




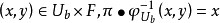
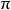





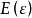


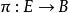
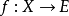

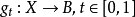
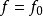

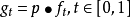
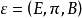
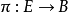
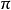

拓撲學中的一種理論。把微分流形及以其上每點為原點的線性獨立的切向量組全體總括在一起得到纖維叢的概念。利用纖維叢理論和連絡幾何學,給出了作為統一電磁場與...
纖維叢論是纖維叢(fibre bundle)向量叢的一般化和推廣。代數拓撲的重要研究對象。...... 纖維叢論是纖維叢(fibre bundle)向量叢的一般化和推廣。代數拓撲的重要研...
纖維叢的理論,是1946年由美國的斯丁路特、美籍華人陳省身、法國的艾勒斯曼共同提出的。數學上,特別是在拓撲學中,一個纖維叢(fiber/fibre bundle)是一個局部看來...
《纖維叢拓撲學》是2011年1月由世界圖書出版公司出版的圖書,作者是Norman Steenrod。本書系統地講述了纖維叢拓撲學等入門知識和深入研究。...
主纖維叢簡稱為主叢,簡記為P(M,G)或P。...... 主纖維叢簡稱為主叢,簡記為P(M,G)或P。 [1] 參考資料 1. 梁燦彬,周彬.微分幾何入門與廣義相對論:科學出...
切纖維叢(tangent fiber bundle)是E流形上的每一點切空間的並所組成的纖維叢。...... 切纖維叢(tangent fiber bundle)是E流形上的每一點切空間的並所組成的...
在數學中,帶有結構群 G(拓撲群)的纖維叢理論允許產生一個配叢,又稱配向量叢(associated bundle)的操作,將叢的典型纖維由 F1 變成 F2,兩者都是具有群 G 作用...
Ck類可微纖維叢(differentiable fiber bundle of class Ck)是轉移函式是Ck可微的纖維叢。...
在數學中,帶有結構群 G(拓撲群)的纖維叢理論允許產生一個配叢(associated bundle)的操作,將叢的典型纖維由 F1 變成 F2,兩者都是具有群 G 作用的拓撲空間。...
主纖維叢上的聯絡(connection on the principalbundle)主纖維叢中鄰近兩點間的一種對應關係,藉此可定義纖維中的一點沿底空間中的一條曲線的平行移動...
1950年法國數學家塞爾利用J.勒雷為研究纖維叢的同調論而發展起來的譜序列這個代數工具,在同倫群的計算上取得突破。從50年代末在代數幾何學和微分拓撲學的影響下產生...
吳大峻發表了論文75c,用不可積相位因子的概念給出了電磁學以及楊—Mills場論的整體描述,討論了Aharonov—Bohm效應和磁單極問題,揭示了規範場在幾何上對應於纖維叢上...
3、國家自然科學青年基金項目:一般非線性系統的纖維叢理論(1993.01-1995.12)[1] 參考資料 1. 慕小武 .鄭州大學[引用日期2019-08-14] ...
1 概念 2 同倫 3 同倫論 4 同倫映射 5 纖維叢理論 同倫提升問題概念 編輯 同倫提升問題(homotopy lift problem)是同倫論的基本問題之一。設連續映射...
從那以後,微分動力系統與遍歷論的普遍溶合和交織,漸漸成為國外離散系統穩定性...3.在纖維叢理論中截面的存在性是引人注目的一個幾何問題。解決這類問題通常可...
├第7章 同調論與 de Rham 上同調論 ├第8章 纖維叢及其拓撲結構 ├第9章 纖維叢上的聯絡與曲率 ├第10章 纖維叢的示性類與曲率張量 第3部分 指標定理和...
關的非線性分析,丘成桐在這方面解決了一系列的問題,微分幾何法也成為理論物理學家的有力工具,楊振寧和米爾斯所提出的規範場理論是物理學中形成的纖維叢上的聯絡論...
