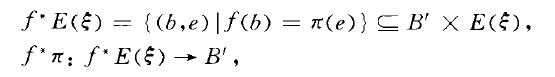
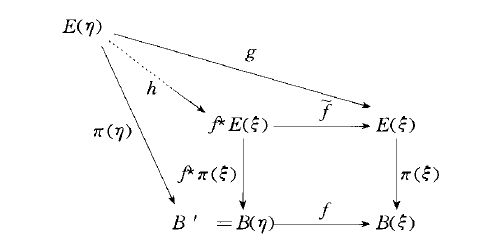
誘導向量叢(induced vector bundle)，亦稱向量叢的回退。由連續映射從一個向量叢按自然方式誘導產生的向量叢，這是構造新向量叢的常用方法之一。
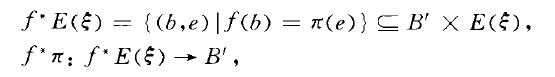
誘導向量叢(induced vector bundle)，亦稱向量叢的回退。由連續映射從一個向量叢按自然方式誘導產生的向量叢，這是構造新向量叢的常用方法之一。設：（E，p，B）為向量叢，.f : B' -＞B為連續映射，...
一個從向量叢π₁:E₁→X₁到向量叢π₂:E₂→X₂的態射（morphism）是一對連續映射f:E₁→E₂和g:X₁→X₂使得 gπ₁= π₂f 對於每個X₁中的x,由f誘導的映射π₁({x}) → π₂({g(x)})是一個向量空間的線性變換。所有向量叢的類和叢的射組成了一個範疇。限制到...
特別地，若ξ=(E，p，B，k，GL(n，R))為向量叢，Δ：B→B×B，Δ(b)=(b，b)為對角映射，則誘導向量叢Δ(ξ₁×ξ₂)稱為向量叢ξ₁，ξ₂的惠特尼和，記為ξ₁⊕ξ₂，而ξ₁⊕ξ₂為B上的n₁+n₂維向量叢。誘導叢在代數拓撲中的一個重要性質是：若B′為仿緊空間，ψ₁，...
記為E⊕F。這兩個向量叢的直和，實際上就相當於對底空間的每一點上的纖維進行線性空間的直和。簡介 設x，y分別是n維，k維向量叢，都以B為底空間，其圖冊分別是Y設 作為圖冊，B是((n+k)維向量叢，稱為x與y的惠特尼和，記為By。而x也可看成積叢BX 由對角映射f;B>BXB決定的誘導叢。
向量叢限制 向量叢限制是一個數學術語。向量叢限制(restriction of vector bundle)一類特殊的向量叢.它是由一個已知的向量叢派生出來的.若(E，p，B)為向量叢，則B是向量叢，稱為在B上的限制，記為可看成包含映射i:B。決定的誘導向量叢.
，對於連續映射:(E＞ E)，若交換，並且對於bEB,Eb是線性映射，則稱為向量叢子到夕的叢同態.進而，若對於(bEB,了Eb+)是同構，則了稱為向量叢同構，此時記為關於向量叢的一個重要事實是:若.f,:B＞B是同倫映射，B'為仿緊空間，則由f，g分別決定的B'上的誘導叢.f' 與g'是叢同構.此定理稱為向量叢的...
設_ (E，Y，B)是向量叢，寧上的一個黎曼度量或內積是指EB，其中+ : En X Eh-R是向量空間E。上的內積(對稱，雙線性的正定二次形式)，並且是連續(或可微)的函式，此時稱+a是正交向量叢.運用單位分解方法，得到:若B是仿緊空間，則B上總存在黎曼度量.在正交向量叢的誘導叢上可以自然方式賦予黎曼度量.
利用cluster理論，實現向量叢穩定範疇中的所有傾斜對象及凝聚層範疇中所有傾斜對象的自同態代數的完全分類。(2)描述權型為(2,2,n)的權投射線上凝聚層範疇中的所有傾斜叢，證明由傾斜叢誘導的從權投射線上凝聚層範疇到相應自同態代數的有限生成模範疇的對應中“丟失的部分”具有abelian範疇的結構。(3)通過給出確切...
它在研究向量叢的分類性質中起重要作用.設GCn,k)是R”中k (1 則向量叢稱為泛向量叢.對於向量叢，一個重要的定理是:若n)k+m，則對於任意m維微分流形M上的k維向量叢寧，都存在連續映射g;M->G(n,k)，使得誘導向量叢 yn=k.這也是y稱為泛叢的原因.
若滿足條件:對於任意bEl3，都存在叢卡(U,卯，使得對於任意二EU,列E.. : E.x}R是將w.}變成R”的同一固定定向的線性同構.若向量叢寧有一個定向。，則稱寧是可定向的.此時('7, w)稱為有向向量叢;否則稱寧是不可定向的.向量叢的可定向性是向量叢的重要拓撲性質.有向向量叢的誘導叢有自然的定向.
Er(八'(T*M)② ),X1,X ,…,X,是M上p個向量場,則 (x x2,...,Xp>Er >.M上R值的p形式就是普通的流形M上的p次外微分形式.向量叢值的外微分形式在微分幾何中使用很多.例如,若f : M->N是光滑映射,則f的微分df就可視為誘導向量叢.f-1TN值的1形式,這裡叢f-'TN-> M在xEM處的纖維是T f ...
對偶叢 對偶叢（dual bundle）是1993年公布的數學名詞。定義 設ξ=π:E→B為n階向量叢，E*=⋃E。對α∈E，令π*(α)=b。存在ξ誘導的自然的n階向量叢ξ*=π*:E*→B。ξ*稱為ξ的對偶叢。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
三是運用模空間的分裂性質證明關於曲線上拋物向量叢模空間上自然線叢的分解定理和消失性定理，進而證明關於上述向量叢整體截面維數的維林德公式。結題摘要 弗羅賓尼烏斯態射是正特徵幾何特有的映射,它誘導出了一系列區別於複數域情形幾何的性質和問題。向量叢的穩定性則是代數幾何中非常基本的概念，其模空間是代數幾何重要...
秩二向量叢陳類c_1, c_2 如果滿足不等式c_1^2＞4c_2, 那么它必定不是半穩定的。這就是著名的波格莫羅夫不等式。 它和代數曲面的宮崗-丘(Miyaoka-Yau)不等式在代數曲面理論中有著廣泛而深刻的套用。波格莫羅夫定理誘導了著名的瑞德(Reider)方法, 為研究某類特殊線性系的性質提供了強有力的工具。它還被...
第一變分公式是計算能量泛函的一階變分公式。若f：M→N是光滑映射，V∈Γ(fTN)是誘導向量叢fTN的一個截面，fₜ：M→N (-ε 的單參數光滑映射族，則當V具有緊緻支集時，成立第一變分公式：式中τ(f)為f的張力場，〈 ， 〉表示N的黎曼內積，*1為M的體積元.這個公式表明τ(f)=0是能量泛函的歐拉-...
映射的第二基本形式（second fundamentalform of a map）由映射確定的重要微分形式.設M和N為黎曼流形，f:M-＞N為光滑映射.記f-`TN為f決定的M上的誘導向量叢。它的誘導聯絡記為守.於是，映射f的第二基本形式a(f)是向量叢T " M⑧T " M⑧.f-' TN的一個截面，定義如下:式中1-'`; I'a,.分別是...
映射的張力場 映射的張力場(tension field of a map)映射的第二基本形式的跡.設f:M->N是黎曼流形M到N的光滑映射.f的第二基本形式a(f)關於M的度量張量的跡稱為映射f的張力場，記為r(f).它是誘導向量叢f-'TN的一個截面，即:(f> Ercf-}TN>.若{e}為M的一個局部么正標架場 ...
第一變分公式是計算能量泛函的一階變分公式。第一變分公式表明：τ(f)=0是能量泛函的歐拉-拉格朗日方程，而調和映射恰是能量泛函的臨界點。簡介 第一變分公式是計算能量泛函的一階變分公式。若f:M→N是光滑映射，V∈Γ(fTN)是誘導向量叢fTN的一個截面，fₜ:M→N(-ε 的單參數光滑映射族，則當V具有緊緻支...
1、對每個實向量叢ξ都相應於一個ξ的底空間B(ξ)的以Z/2為係數的上同調類序列 稱為ξ的斯蒂弗爾-惠特尼類。類ω₀(ξ)等於單位元1∈H⁰(B(ξ);Z/2)，而若ξ是n-平面叢，對於大於n的i，ω(ξ)=0。2、自然性。若f:B(ξ)→B(η)被從ξ到η的一個叢映射覆蓋，則 f*為f誘導的同態。3、...
