施蒂費爾-惠特尼類(Stiefel-Whitney classes)是向量叢的底空間的上同調類。
基本介紹
- 中文名:施蒂費爾-惠特尼類
- 外文名:Stiefel-Whitney classes
- 適用範圍:數理科學
簡介
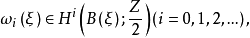
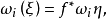
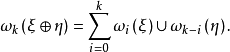
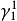
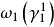
施蒂費爾-惠特尼類(Stiefel-Whitney classes)是向量叢的底空間的上同調類。
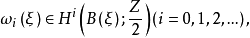
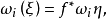
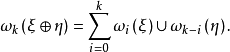
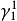
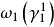
施蒂費爾-惠特尼類(Stiefel-Whitney classes)是向量叢的底空間的上同調類。...... 施蒂費爾-惠特尼類(Stiefel-Whitney classes)是向量叢的底空間的上同調類。...
惠特尼對偶定理(Whitney duality theorem)是微分流形的切叢與餘切叢的施蒂費爾-惠特尼類的關係。...
惠特尼還給出示性類的形式冪級數以及偶示性類的概念.至此,施蒂費爾-惠特尼示性類的理論基礎正式建立.其後,J.米爾諾(Milnor)以惠特尼提出的四個定理為公理開展示...
惠特尼乘積定理(Whitney product theorem)屬於惠特尼與吳文俊,由惠特尼乘積定理可定義施蒂費爾-惠特尼類。...
全施蒂費爾-惠特尼類(total Stiefel-Whitney class)是各階施蒂費爾-惠特尼類之和。...... 全施蒂費爾-惠特尼類(total Stiefel-Whitney class)是各階施蒂費爾-惠特尼...
示性類(characteristic class),數學名詞,示性類理論的基本概念.。施蒂費爾一惠特尼類、陳類、龐特里亞金類等統稱為示性類.施蒂費爾一惠特尼數、陳數、龐特里亞金數...
示性類理論是流形上的分析(即大範圍分析學)的一個分支,也是拓撲學的一個分支,最早的創始者是施蒂費爾(Stiefel,E.L.)和惠特尼(Whitney,H.)。...
施蒂費爾-惠特尼數、陳數、龐特里亞金數等總稱為示性數。乘法示性類乘法序列 編輯 (multiplicative sequence)乘法序列是多項式構成的一個序列,設∧是一個固定的有...
2.若把 的定向反向,則歐拉類 變號。3.若纖維維數n是奇數,則4.自然同態 把歐拉類 變為施蒂費爾一惠特尼類 。5.惠特尼和的歐拉類滿足 。類似地,笛卡兒積的...
定向配邊類定向配邊不變數 兩個定向閉流形定向配邊若且唯若其所有的施蒂費爾-惠特尼示性數和龐特里亞金示性數對應相等。的具體結構如下:...
纖維叢的截面的存在性問題與阻礙理論有關,由此得到底空間的某些上同調類,稱之為示性類。施蒂費爾、惠特尼、陳省身和原蘇聯數學家龐特里亞金、中國數學家吳文俊都...
的配邊類。(3)配邊的充分必要條件 兩流形配邊若且唯若其每個施蒂費爾-惠特尼示性數對應相等。配變理論定向配邊理論 編輯 定向配邊理論的研究對象是所有定向流...
