偏微分方程(廈門大學建設的慕課)

偏微分方程是廈門大學建設的慕課、國家精品線上開放課程，該課程於2017年3月1日在中國大學MOOC首次開設，授課教師為譚忠。據2021年7月中國大學MOOC官網顯示，該課程已開課9次。

該課程共8章，包括引言：從音樂審美到揭秘量子糾纏；典型偏微分方程模型的建立；偏微分方程的基本概念、形成的數學問題與分類；高維波動方程的Cauchy問題；能量方法、極值原理與格林函式法等章目。

基本介紹

• 中文名：偏微分方程
• 外文名：Partial Differential Equations（PDE）
• 類別：慕課、國家精品線上開放課程
• 建設院校：廈門大學
• 開課平台：中國大學MOOC
• 授課教師：譚忠
• 首開時間：2017年3月1日

課程性質

課程背景

21世紀，人類社會仍有7個千禧年大獎難題，其中龐加萊猜想、Navier-Stokes方程的整體光滑解的存在性、黎曼猜想、N體問題等4個問題與偏微分方程理論直接相關。該課程是較為古老的一門課程，誕生於十八世紀中葉的微積分。但該課程的思想源於公元前490年的古希臘哲學家、數學家畢達哥拉斯的音樂審美。同時偏微分方程是一門新穎的學科，隨著人類社會的發展，它在各行各業中出現了較為新穎的偏微分方程形式。

課程定位

偏微分方程課程從“音樂審美”到“瑪雅預言”，從心靈感應到“量子糾纏”均有展現。同時是金融工程學科以及航空航天工程的奠基課程，是本科數學各類課程的核心，其他課程與該課程均有聯繫，或與該課程聯繫後可以產生其他分支課程。該課程是從微積分通往偏微分方程理論研究和其實際套用的重要驛站，既可以訓練與提高微積分水平，又可以拓寬大學生的就業渠道，提高大學生的創新意識與創新能力。

課程定位

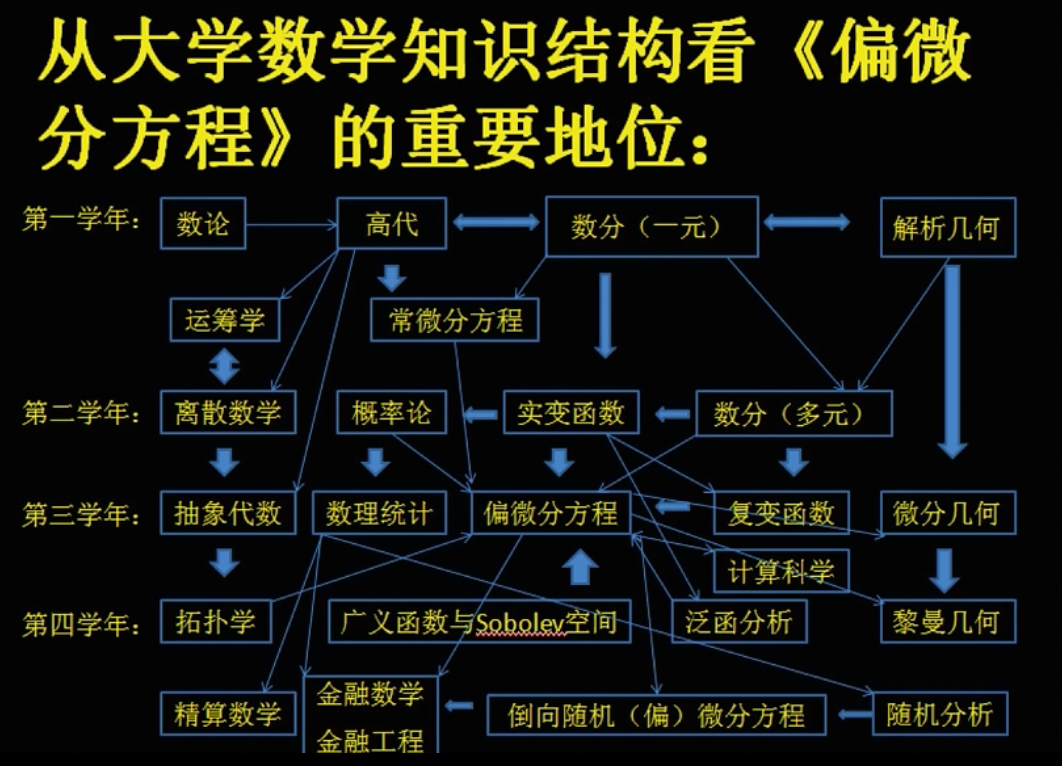
適應對象

該課程可作為高等院校本科生“偏微分方程”“數學物理方程”的線上學習課程，也可作為理工科和經濟管理學科本科生、研究生的線上學習課程。

課程簡介

該課程根據課程負責人多年為數學專業大學生講授“數學物理方程”和“偏微分方程”課程的基礎上，汲取中國國內外前沿同類較為優秀教材的案例製作而成。課程共分8章，包括：（1）引言與偏微分方程建模；（2）偏微分方程一般概論；（3）求解波動方程的Cauchy問題（D'Alembert公式）；（4）分離變數法；（5）Fourier變換法；（6）能量方法與極值原理。

課程大綱

開課信息

課程特色

該課程刻畫偏微分方程這門學科產生的歷史源頭問題以及在世界的實用性，選編了歷史上經典案例，還選編了現實感較強的案例進行分析，讓同學們感受到這門課程的理論價值，還希望能讓學習者感受這門學科的時代感和所具有的社會的、現實的價值。

教學計畫

時間	章目	教學內容	教學要求
第1周	從音樂審美到揭秘瑪雅預言--偏微分方程的巨大威力	什麼是偏微分方程？它為什麼產生？產生三類典型偏微分方程的源頭問題是什麼？現代提法怎樣？如何建立三類典型偏微分方程？	了解偏微分方程產生的歷史與源頭問題，了解建立三類典型偏微分方程的基本假設與方法，掌握建模方法。
第2周	偏微分方程一般概念	對兩個變數的二階偏微分方程進行分類。三類典型偏微分方程中涉及的初始（Chauchy）問題、初邊值問題（Initial-boundary value problem）、邊界值問題（Boundary value problem）。	掌握兩個變數的二階偏微分方程進行分類方法。掌握三類典型偏微分方程初始（Chauchy）問題、初邊值問題（Initial-boundary value problem）、邊界值問題（Boundary value problem）。
第3周	D'Alembert公式	線性疊加原理、齊次化原理（Duhamel原理）、D'Alembert公式、左傳播波、右傳播波。	掌握線性疊加原理和齊次化原理（Duhamel原理），掌握D'Alembert公式的推導方法，了解左傳播波和右傳播波。
第4周	分離變數法	一維Sturm-Liouville 問題、初等Fourier級數，套用分離變數法分別對波動方程、熱傳導方程和矩形區域Dirichlet邊界的調和方程。	掌握一維Sturm-Liouville 問題的求解，掌握Fourier級數的基本公式，掌握套用分離變數法分別對波動方程、熱傳導方程和矩形區域Dirichlet邊界的調和方程求解。
第5周	Fourier變換法	Fourier 變換的性質、用 Fourier 變換法求解波動方程的初值問題、用 Fourier 變換方法求解熱傳導方程的初值問題。	掌握Fourier 變換的性質、掌握套用 Fourier 變換法求解波動方程的初值問題、掌握套用 Fourier 變換方法求解熱傳導方程的初值問題。
第6周	能量方法與極值原理	Gauss 和 Green 公式、分部積分公式、能量方法與三類典型方程的唯一性。調和方程的極值原理、線性熱方程的極值原理。	熟練掌握Gauss 和 Green 公式、分部積分公式、能套用能量方法證明簡單三類典型方程的唯一性。熟練掌握調和方程的極值原理、線性熱方程的極值原理、能套用極值原理法證明調和方程和線性熱方程的的唯一性。

（註：此為課程第1~2次開課教學計畫）

教學目標

1、了解偏微分方程模型的來源、掌握偏微分方程建模方法，並了解其基本概念和基本問題；

2、熟練掌握套用行波法、分離變數方法、Fourier變換法和Green函式法求解三類典型方程以及基本解及其性質和極值原理和能量方法；

3、訓練用高維分部積分公式解決偏微分方程的前沿問題。

學習預備

預備知識

學習偏微分方程課程需要具備高等數學、高等代數、解析幾何、常微分方程等知識。

學習資料

• 課程教材

書名	作者	ISBN	出版時間	出版社
《偏微分方程——現象、建模、理論與套用》	譚忠	9787040529012	2020年1月	高等教育出版社出版

• 其他資料

【1】Deutsch. Partial Differential Equations through Examples and Exercises - Springer[J]. Springer Netherlands.

【2】姜禮尚、吳蘭成.數學物理方程講義[M].北京:高等教育出版社,2007.

【3】Partial Differential Equations, L.C.Evans, American Mathematical Society Providence,Rhode Island.3

【4】Linear Partial Differential Equations for Scientists and Engineers，Tyn Myint-U，Lokenath Debnath，Fourth Edition，2007 Birkha¨user Boston，ISBN-10: 0-8176-4393-1.

考核標準

1、完成5次主觀題作業（互評） （40%）

完成主觀題作業後，應參加作業的互評，互評要求：每人應完成5份他人作業的互評，未參加互評的學生，將給與所得分數的50%；參加互評，但未達到5份的，將給與所得分數的80%；

2、完成考試（提交分享報告，互評） （60%）。

分數達到60分，可申請合格證書；分數達到80分的，可申請優秀證書。

所獲榮譽

2019年1月8日，該課程被中華人民共和國教育部認定為“2018年國家精品線上開放課程”。

教師簡介

譚忠，男，廈門大學“閩江學者”特聘教授、博士生導師，國務院政府特殊津貼，全國百篇優秀博士論文指導教師；主持國家自然科學基金重點項目，主持國家精品共享課程“數學建模”，福建省教學名師獎和寶鋼優秀教師獎獲得者；福建省套用數學重點學科學科帶頭人；首屆廈門大學新世紀優秀人才；廈門市重點人才。