基本介紹
- 中文名:依分布收斂
- 外文名:convergenceindistribution
- 所屬學科:數學
- 相關概念:隨機變數序列、依機率收斂等
定義
定義1



定義2




實例分析

















相關定理
定理1

定理2





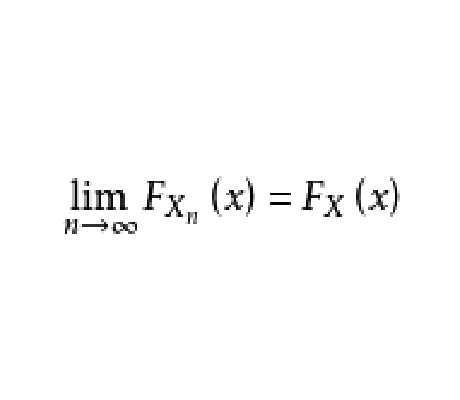






























依分布收斂是隨機變數列的一種收斂性,設{ξn,n≥1}是機率空間(Ω,F,P)上的隨機變數列,其相應的分布函式列為{Fn(x),n≥1},如果Fn(x)弱收斂於隨機變數ξ的分布函式F(x),則稱隨機變數列ξn依分布收斂到...
分布弱收斂是機率論和數理統計中經常用到的一種收斂性。中心極限定理就是討論隨機變數序列的標準化部分和依分布收斂於正態隨機變數的定理。大樣本統計中也要討論各種統計量依分布收斂的問題。設{(),≥1}為分布函式列,而()為一非降...
常見收斂性 依分布收斂 亦稱“弱收斂”,稱隨機變數列依分布收斂於隨機變數X,記作Xₙ⇒X,如果在X的分布函式 F(x)的每一連續點x上,Xₙ的分布函式Fₙ(x)收斂於F(x)。依機率收斂 亦稱“隨機收斂”。稱隨機變數列{Xₙ...
與函式列的收斂性不同,隨機變數列的收斂性是在機率意義下的收斂性。最常用的是:依分布收斂、依機率收斂,以機率1收斂和r階平均收斂……後兩種收斂性要強於前兩種,但後兩種之間並無確定強和弱的關係。
依機率收斂是一種常見的收斂性質。依機率收斂比依分布收斂更強,比平均收斂則要弱。如果一個隨機變數序列依機率收斂到某一個隨機變數,則它們也一定依分布收斂到這個隨機變數。反過來則不然:只有當一個隨機變數序列依分布收斂到一個常數...
存在一個吸收域,即存在一個獨立同分布的隨機變數序列 以及序列 使得 則稱隨機變數X是一個穩定分布。此定義也稱廣義中心極限定理,其中“”表示依分布收斂。特別地,如果 滿足獨立同分布且具有有限方差,則高斯分布是其極限分布,式(3)...
以機率1收斂和r階平均收斂不能互推。如果ξn是獨立隨機變數序列{Yn,n≥1}的部分和,那么依分布收斂、依機率收斂和以機率1收斂是等價的。經典的極限理論研究(正則化的)獨立隨機變數序列部分和的各種收斂性。至20世紀40年代,基本結果...
依機率收斂是一種常見的收斂性質。依機率收斂比依分布收斂更強,比平均收斂則要弱。如果一個隨機變數序列依機率收斂到某一個隨機變數,則它們也一定依分布收斂到這個隨機變數。反過來則不然:只有當一個隨機變數序列依分布收斂到一個常數...
依機率收斂到0。證明方法:用Taylor展開特徵函式,證明其收斂到常數,得到依分布收斂,然後再用依分布收斂到常數等價於依機率收斂。現代機率 (3) 精確弱大數定律:若xP(|X|>x) 當x趨於無窮時收斂到0,則 依機率收斂到0,其中 ...
依分布收斂於標準常態分配N(0,1)。基於這個性質可知, 當n較大時,可用 作為 μ 的區間估計,其中 是標準常態分配的上 分位數(見機率分布);這個估計的置信係數當n→ 時趨於指定的 1-α(0<α<1)。這就是一個大樣本...
用表示在【0,1】上導出的機率分布,表示由布朗運動={(): 0≤≤1}在【0,1】上導出的機率分布(通常稱為維納測度),那么當趨於∞時,{,≥1}弱收斂到。這時,也稱隨機過程式列{,≥1}依分布收斂到,記作同樣,這一結果之所以稱為...
,xn為抽自參數為p的二點分布的樣本,當n→∞時,依分布收斂(見機率論中的收斂)於標準常態分配N(0,1),以 uα/2記N (0,1)的上 α/2分位數。所以,可作為p的一個區間估計,上面的極限值1-α就定義為它的漸近置信...
2.1 依機率收斂 2.2 大數定律 §3 中心極限定理 3.1 依分布收斂 3.2 中心極限定理 習題五 第六章 樣本及樣本函式的分布 §1 總體與樣本 1.1 總體 1.2 簡單隨機樣本 §2 直方圖與樣本分布函式 2.1 直方圖 2.2 樣本分布...
6.1 依機率收斂與平均收斂 293 6.1.1 依機率收斂 293 6.1.2 平均收斂 299 6.2 依分布收斂 306 6.2.1 依分布收斂的概念 306 6.2.2 連續性定理及其套用 309 6.3 弱大數律和中心極限定理 314 6.3.1 弱大數律 315 6...
同分布,則稱 為無窮可分點過程。利用隨機測度理論,無窮可分點過程的表征問題得到了比較徹底的解決。套用 隨機測度的收斂與極限問題相應於測度序列的各種收斂性,可以定義隨機測度(隨機點過程)的弱收斂、強收斂、淡收斂、依分布收斂等...
6.1 隨機向量及聯合分布 6.2 均勻分布與常態分配 6.3 隨機向量的函式的分布 第七章 隨機序列的收斂 7.1 收斂的不同意義 7.2 強大數定律 7.3 Kolmogorov不等式與強大數律(*)7.4 一致可積性(*)7.5 依分布收斂 第八章 ...
1.2 依機率收斂 1.3 大數定律 2 中心極限定理 2.1 依分布收斂 2.2 中心極限定理 習題五 第六章 樣本及樣本函式的分布 1 總體與樣本 1.1 總體 1.2 簡單隨機樣本 2 直方圖與樣本分布函式 2.1 直方圖 2.2 樣本分布函式 3...
3.1 依機率收斂 3.2 幾乎必然收斂 3.3 r階中心矩收斂 3.4 依分布收斂 3.5 各種收斂方式之間的關係 3.6 漸近理論中的基本工具 3.7 隨機數的產生 3.8 習題 第4章 數據壓縮技術 4.1 點估計量的優劣判斷 4.2 ...
5.5收斂的概念212 5.5.1依機率收斂212 5.5.2殆必收斂213 5.5.3依分布收斂215 5.5.4Δ方法219 5.6生成隨機樣本224 5.6.1直接法225 5.6.2間接法229 5.6.3舍選法230 5.7習題232 5.8雜錄245 5.8.1中心極限定理...
5.1 依機率收斂與大數定律 5.1.1 依機率收斂 5.1.2 大數定律 5.2 中心極限定理 5.2.1 依分布收斂 5.2.2 中心極限定理 習題5 第6章 數理統計基本知識 6.1 總體與樣本 6.1.1 總體和樣本 6.1.2 什麼是統計學 6....
5.3 依分布收斂和中心極限定理 .125 5.4 習題 130 第 6 章 常態分配的導出分布 133 6.1 引言 133 6.2 .2 分布、t 分布和 F 分布 133 6.3 樣本均值和樣本方差 .134 6.4 習題 136 第 7 章 抽樣調查 138 7.1 ...
§5.2 依機率收斂及依分布收斂 §5.3 弱大數定律 §5.4 中心極限定理 習題五 附錄1 關於確定測量偶然誤差機率密度函式的一種推導方法 附錄2 關於連續型隨機變數函式數學期望公式的一種證法 附錄3 運用標準分數確定個體成績在團體或...
習題七 第8章 大數定律與中心極限定理及其套用 8.1 大數定律 8.1.1 切比雪夫不等式 8.1.2 依機率收斂 8.1.3 大數定律 8.2 中心極限定理 8.2.1 依分布收斂 ……第9章 隨機過程 第10章 SPSS的簡單套用 附錄 ...
三、分布函式的可加性 四、多元特徵函式 第五節 多元常態分配 一、密度函式 二、特徵函式與數字特徵 三、獨立性 四、線性變換與條件分布 習題四 第五章 大數定律和中心極限定理 第一節 隨機變數序列的四種收斂性 一、依分布收斂 ...
一階有效估計是一致最優漸近正態估計量。拉奧(RaoC. R. )建議只考慮依分布一致收斂於正態估計的相合漸近正態估計量,並且證明:在一-定正則性條件下,這種估計量漸近方差都不會小於克拉默:拉奧方差界。這樣的估計稱一致漸近正態...
5.1.2 依機率收斂141 5.1.3 大數定律142 5.2 中心極限定理144 5.2.1 依分布收斂144 5.2.2 中心極限定理145 習題5150 第6章 數理統計的基本知識152 6.1 總體與樣本152 6.1.1 總體152 6.1.2 樣本153 6.2 直方圖與...
隨機測度的收斂與極限問題相應於測度序列的各種收斂性,可以定義隨機測度(隨機點過程)的弱收斂強收斂、淡收斂、依分布收斂等(見機率論中的收斂),=。並可研究其相互關係,從而進一步研究在一定條件下隨機測度序列收斂到某個特殊隨機測度的問...
