隨機過程的極限定理是討論一列隨機過程的機率分布和樣本函式極限性質的一類定理。
基本介紹
- 中文名:隨機過程的極限定理
- 類型:討論一列隨機過程的機率分布和樣本函式極限性質的一類定理
基本信息
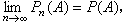
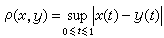
其他信息
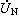
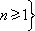
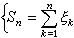
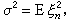
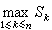
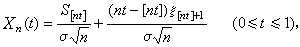
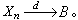
隨機過程的極限定理是討論一列隨機過程的機率分布和樣本函式極限性質的一類定理。
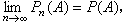
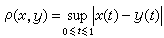
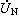
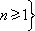
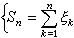
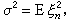
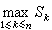
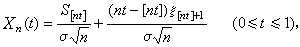
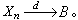


隨機過程的極限定理是討論一列隨機過程的機率分布和樣本函式極限性質的一類定理。基本信息在實值隨機過程樣本函式所構成的函式空間(簡稱樣本空間)上,依不同情況引進函式間的距離,使它成為度量空間,隨機過程式列={(),∈},=1...
隨機過程用的極限定理 《隨機過程用的極限定理》是世界圖書出版公司北京公司出版的圖書,作者是傑克德 (Jean Jacod)
1對應於隨機過程的測度 2距離空間中的測度 3線性空間上的測度 特徵泛函 4在空間□p中的測度 5Hilbert空間中的測度 6Hilbert空間中的Gauss測度 第六章關於隨機過程的極限定理 1距離空間中測度的弱收斂 2Hilbert空間中測度弱收斂的條件 ...
《多參數隨機過程和隨機場的極限理論》是依託浙江大學,由張立新擔任項目負責人的青年科學基金項目。項目摘要 本項目研究了多指標隨機場和Gauss過程的極限理論。內容包括:實值和B值混合隨機場的強極限定理以及抽象空間上混合隨機場的極限...
中國學者在平穩過程、馬爾科夫過程、鞅論、極限定理、隨機微分方程等方面做出了較好的工作。數學上的隨機過程是由實際隨機過程概念引起的一種數學結構。給定機率空間 (Ω, F, P),隨機變數 X(ω) 是定義在樣本空間 Ω 上,取值於...
第1章隨機過程的基本概念和基本類型 1.1基本概念 1.2有限維分布與Kolmogorov定理 1.3隨機過程的基本類型 習題1 第2章Poisson過程 2.1Poisson過程的定義和性質 2.2與Poisson過程相聯繫的若干分布 2.2.1Xn和Tn的分布 2.2.2事件...
《關於樹指標隨機過程極限理論的進一步研究》是依託江蘇大學,由楊衛國擔任項目負責人的面上項目。項目摘要 本項目研究在一般狀態空間取值的樹指標馬氏鏈的強大數定律、熵遍歷定理與中心極限定理;二叉樹上在一般狀態空間取值的非齊次分支馬氏...
本書第一卷系統介紹隨機函式論和函式空間測度理論的一般問題.共分八章,包括機率論的基本概念,隨機序列,隨機函式,隨機過程線性理論,函式空間上的機率測度,隨機過程的極限定理,對應於隨機過程的測度的絕對連續性Hilbert空間上的可測...
出於擴大極限定理套用範圍的目的,馬爾科夫在本世紀初開始考慮相依隨機變數序列的規律,並從中選出了最重要的一類加以研究。1906年他在《大數定律關於相依變數的擴展》一文中,第一次提到這種如同鎖鏈般環環相扣的隨機變數序列,其中某個...
§1.4 中心極限定理……… 35 §1.5 特徵函式……… 37 §1.6 矩母函式及母函式……… 40 習題 ……… 43 第二章 隨機過程預備知識 ……… 46 §2.1 條件期望……… 46 §2.1.1 事件域與...
1.6.2 二維隨機變數函式的分布 36 1.6.3 隨機變數函式的數字特徵 38 1.6.4 隨機變數的特徵函式 40 1.7 大數定理與中心極限定理43 1.7.1 大數定律43 1.7.2 中心極限定理 46 習題一 47 第二章 隨機過程的基本概念 ...
第1章 隨機事件和機率 第2章 隨機變數及其分布 第3章 多維隨機變數及其分布 第4章 隨機變數的數字特徵 第5章 極限定理 第6章 樣本及抽樣分布 第7章 參數估計 第8章 假設檢驗 第9章 方差分析與回歸分析 第10章 隨機過程的一般...
《依時隨機環境中的實值分枝隨機遊動的極限定理》是依託哈爾濱工業大學,由黃春茂擔任項目負責人的青年科學基金項目。項目摘要 本項目擬研究依時隨機環境中在實數空間R^d中取值的分枝隨機遊動的極限定理及相關漸近性質。我們首先考察空間...
1.5.2 獨立隨機變數和的分布 1.5.3 條件期望 第2章 隨機過程的基本概念和基本類型 2.1 基本概念 2.2 有限維分布與Kolmogorov定理 2.3 隨機過程的基本類型 2.3.1 平穩過程 2.3.2 獨立增量過程 習題二 第3章 Poisson過程 ...
11.1.2 隨機變數5 1.1.3 黎曼-斯蒂爾切斯積分10 1.1.4 數字特徵13 1.1.5 矩母函式、特徵函式15 1.1.6 幾個重要的極限定理17 習題 1.1.191.2 隨機過程的基本概念 191.2.1 隨機過程的定義 191.2.2...
}或{xt,t≥0},它是從一個隨機過程抽得的樣本。為了得到描述這一隨機過程變化的統計規律,必須對它的分布(見機率分布)或某些特徵作出推斷。例如檢驗它是否為某種特殊的隨機過程,估計其分布中的某些參數等等。這些都屬於隨機過程的統計...
《隨機過程》是2021年科學出版社出版的圖書。內容簡介 本書以隨機過程的統計特徵和性質為主線,旨在將實際套用和理論推導聯繫起來,通過概念、定理、例題、詳細的習題,儘量體現隨機過程的理論基礎及套用價值,以保證教材的綜合性、整體性和前瞻...
1.4 極限定理 1.4.1 馬爾可夫不等式和切比雪夫不等式 1.4.2 大數定律與中心極限定理 1.4.3 更一般的極限定理 第一章小結 習題 第二章 隨機過程的基本概念和基本類型 2.1 隨機過程的基本概念 2.1.1 基本概念 2.1...
何書元,博士、北京大學數學科學學院教授,從事套用隨機過程、時間序列分析和機率極限定理的教學和科研工作。主講課程有機率論、機率統計、套用隨機過程、套用時間序列分析和極限定理等。兼任教育部數學與統計學教學指導委員會委員、全國統計教材...
1.2 隨機變數與分布函式 1.3 數字特徵、矩母函式與特徵函式 1.4 收斂性 1.5 獨立性與條件期望 第2章 隨機過程的基本概念和基本類型 2.1 基本概念 2.2 有限維分布與Kolmogorov定理 2.3 隨機過程的基本類型 習 題 第3章 ...
1.4.4獨立隨機變數和的分布16 1.5收斂性17 第2章隨機過程的基本概念和基本類型20 2.1基本概念20 2.2有限維分布與Kolmogorov定理21 2.3隨機過程的基本類型24 2.3.1平穩過程24 2.3.2獨立增量過程30 習題31 第3章Poisson過程32...
布朗橋是連續時間的隨機過程B(t) ,在 B(0)= B(1)= 0的條件下,它的機率分布服從維納過程W(t)的條件機率分布。是討論一列隨機過程的機率分布和樣本函式極限性質的一類定理。布朗橋定義 {B(t), }為標準布朗運動,不妨...
在人類發展的歷史上,馬爾可夫鏈是第一個從理論上被提出並加以研究的隨機過程模型。馬爾可夫鏈的提出來自俄國數學家安德雷·馬爾可夫(Андрей Андреевич Марков)。為了擴大機率論極限定理的套用範圍,1906年,...
