基本介紹
複變函數

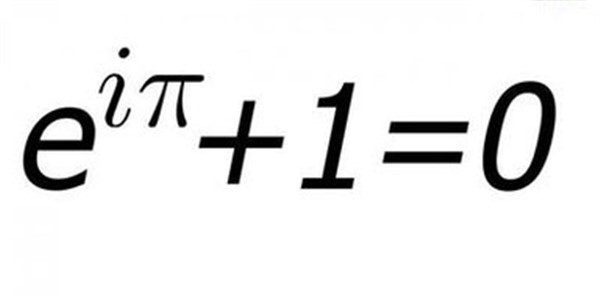
歐拉公式證明



















拓撲學


拓撲學證明
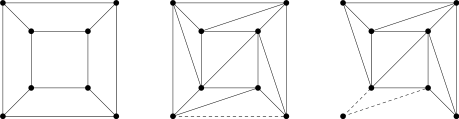
- 若有一個多邊形面有3條邊以上,我們劃一個對角線。這增加一條邊和一個面。繼續增加邊直到所有面都是三角形。
- 除掉只有一條邊和外部相鄰的三角形。這把邊和面的個數各減一而保持頂點數不變。
- (逐個)除去所有和網路外部共享兩條邊的三角形。這會減少一個頂點、兩條邊和一個面。
分式

平面幾何










統計學
物理學


Euler公式一般指本詞條

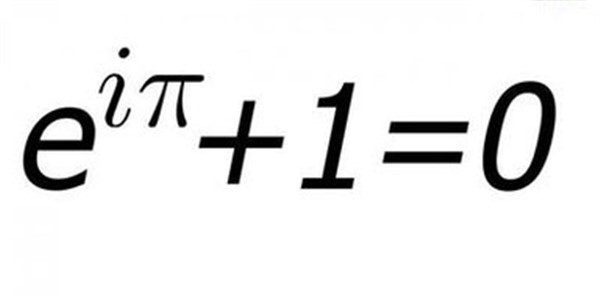


































在數論中,歐拉定理(Euler Theorem,也稱費馬-歐拉定理或歐拉函式定理)是一個關於同餘的性質,實際上是費馬小定理的推廣。複數中的歐拉定理也稱為歐拉公式,被認為是數學世界中最美妙的定理之一。此外還有平面幾何中的歐拉定理、多面體歐拉...
翻譯的歐拉公式 V + F - E = 2 的19種證明方法 (原文: Nineteen Proofs of Euler's Formula )"我"的話:1. 若論思想性、精簡、嚴密, 原文遠勝。 所以贅述, 乃體諒中文資料難求之苦。2. 歡迎修改 注:1.帶引號的詞語,...
證明:由內切圓、外接圓的半徑公式中消去S得 利用正弦定理,把邊長化為角度得 左邊利用二倍角公式,右邊利用三角形三角函式特殊關係化簡得 整理得 △ABC的內切圓、外接圓半徑分別為 r,R,大家知道有著名的 Euler公式:R ≥ 2 r。
歐拉-麥克勞林公式(Euler-Maclaurin formula)是有關定積分的一種數值計算公式,它建立了函式的積分與其導數的聯繫。在數值積分理論與級數求和法中,Euler-Maclaurin公式是一個極有用的工具。基本介紹 歐拉-麥克勞林公式 設函式f(x)在區間[...
可以改寫為矩陣形式,被廣泛套用於空間解析幾何和計算機圖形學領域,成為剛體運動的基本計算公式。發現歷程和定義 在向量旋轉公式發現以前,瑞士數學家列昂哈德·歐拉(Leonhard Euler(1707-1783))為了證明四平方和定理,發現了四平方和恆等式...
歐拉-龐加萊公式 歐拉-龐加萊公式(Euler-Poincare&1& formula)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
瑞士數學家歐拉(Euler, L.)則於1771年以 及於1778年以 表示由n個不同元素中每次取出p個元素的組合數。1830年,英國數學家皮科克(Peacock, G)引入符號Cr表示n個元素中每次取r個的組合數。1869年或稍早些,劍橋的古德文以符號...
歐拉(Euler)算法是數值求解中最基本、最簡單的方法,但其求解精度較低,一般不在工程中單獨進行運算。歐拉算法 所謂數值求解,就是求問題的解y(x)在一系列點上的值y(xi)的近似值yi。對於常微分方程:可以將區間[a,b]分成n段,...
公式介紹 歐拉常數(Euler-Mascheroni constant)歐拉-馬歇羅尼常數(Euler-Mascheroni constant)是一個主要套用於數論的數學常數。它的定義是調和級數與自然對數的差值的極限。由無窮級數理論可知,調和級數 是發散的。但可以證明, 存在極限...
在運動學裡,歐拉旋轉定理(Euler's rotation theorem)表明,在三維空間裡,假設一個剛體在做一個旋轉的時候,剛體內部至少有一點固定不動,則此位移等價於一個繞著包含那固定點的固定軸的旋轉。這定理是以瑞士數學家萊昂哈德·歐拉命名...
歐拉法是常微分方程的數值解法的一種,其基本思想是疊代。其中分為前進的EULER法、後退的EULER法、改進的EULER法。所謂疊代,就是逐次替代,最後求出所要求的解,並達到一定的精度。誤差可以很容易地計算出來。歐拉法是考察流體流動的一...
歐拉積分是由瑞士數學家萊昂哈德·歐拉(Leonhard Euler , 1707.4.15~1783.9.18)整理得出的兩類特殊的含參變數的積分。由歐拉積分所定義的函式分別稱為伽馬函式和貝塔函式。它們對於積分的簡便運算有重要的運用。基本信息 含參量積分 ...
歐拉級數是各項為質數倒數的級數,歐拉(Euler,L.)於1748年證明了歐拉級數是發散的,同時給了質數集是無窮集的一個證明。簡介 歐拉級數是各項為質數倒數的級數,即級數 ,式中pₙ為第n個質數。背景 歐拉(Euler,L.)於1748年...
定義 稱(k₁ + k₂)/2為曲面在一點處的平均曲率,記為 它描述了曲面在一點處的平均彎曲程度,又稱為中曲率。根據韋達定理,由主曲率的計算公式,易知 推論 曲面在橢圓點處K > 0,雙曲點處K < 0,拋物點處K = 0。
與歐拉公式的聯繫 如果把棣莫弗定理和歐拉(Euler)公式 (參見《泰勒公式》,嚴格的證明需要複分析)放在一起看,則可以用來理解歐拉公式的意義。利用棣莫弗定理有:如果可以把所有的複數改寫成指數的形式,即 則 這和指數的可加性...
歐拉連乘積公式 歐拉常數最先由瑞士數學家萊昂哈德·歐拉(Leonhard Euler)在1735年發表的文章 De Progressionibus harmonicus observationes 中定義。歐拉曾經使用C作為它的符號,並計算出了它的前6位小數。1761年他又將該值計算到了16位...
歐拉分式是一種特殊的分式。歐拉對數學的研究廣泛,因此在許多數學的分支中也可經常見到以他的名字命名的重要常數、公式和定理。此外歐拉還涉及建築學、彈道學、航海學等領域。簡介 歐拉分式是一種特殊的分式。設a,b,c是不同的常數,...
歐拉 (Euler,L.) 計算過 與 是等價無窮大,更準確地,有 ,其中 C=0.577 215... 是歐拉常數,。這是歐拉於1740 年發現的,更一般地,級數 稱為廣義調和級數,亦簡稱調和級數,它的通俗名稱是 p 級數,當 p>1 時收斂,p ...
1.1Euler方程 1.2無旋流和非線性波方程 1.3變分方程和聲學度量 1.4基本變分 第二章基本幾何構造 2.1與聲學度量相關的類葉狀結構 2.1.1Galileo時空 2.1.2類葉狀結構和聲學坐標 2.2函式H的幾何解釋 第三章聲學結構方程 3.1...
自然常數,符號e,為數學中一個常數,是一個無限不循環小數,且為超越數,其值約為2.718281828459045。它是自然對數函式的底數。有時稱它為歐拉數(Euler number),以瑞士數學家歐拉命名;也有個較鮮見的名字納皮爾常數,以紀念蘇格蘭...
