歐拉級數是各項為質數倒數的級數,歐拉(Euler,L.)於1748年證明了歐拉級數是發散的,同時給了質數集是無窮集的一個證明。
基本介紹
- 中文名:歐拉級數
- 外文名:Euler series
- 適用範圍:數理科學
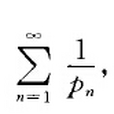
歐拉級數是各項為質數倒數的級數,歐拉(Euler,L.)於1748年證明了歐拉級數是發散的,同時給了質數集是無窮集的一個證明。
歐拉級數是各項為質數倒數的級數,歐拉(Euler,L.)於1748年證明了歐拉級數是發散的,同時給了質數集是無窮集的一個證明。簡介歐拉級數是各項為質數倒數的級數,即級數,式中pn為第n個質數。背景歐拉(Euler,L.)...
當級數 收斂時,級數 也收斂,且有相同的和。若所有aₙ>0,且 關於k單調,(q是某個常數),則級數 比級數 收斂得快。套用 當級數 發散時,級數 仍可能收斂。在級數 收斂於S時,級數 稱為歐拉可和,且稱S為它的歐拉和。例...
奇函式,可以表示為正弦級數,而偶函式,則可以表示成餘弦級數:只要注意到歐拉公式:,這些公式便可以很容易從上面傅立葉級數的公式中導出。廣義傅立葉級數 類似於幾何空間上矢量的正交分解,周期函式的傅立葉級數是在內積空間上函式的...
歐拉常數(Euler-Mascheroni constant)歐拉-馬歇羅尼常數(Euler-Mascheroni constant)是一個主要套用於數論的數學常數。它的定義是調和級數與自然對數的差值的極限。由無窮級數理論可知,調和級數 是發散的。但可以證明, 存在極限。由不等式...
這一公式是瑞士數學家 Leonhard Euler 在1737 年的一篇題為《對無窮級數的若干觀察》的論文中提出並加以證明的, 式中的 n 為自然數 (即正整數),p 為素數。歐拉乘積公式將一個對自然數的求和表達式與一個對素數的連乘積表達式聯繫...
歐拉-麥克勞林公式(Euler-Maclaurin formula)是有關定積分的一種數值計算公式,它建立了函式的積分與其導數的聯繫。在數值積分理論與級數求和法中,Euler-Maclaurin公式是一個極有用的工具。基本介紹 歐拉-麥克勞林公式 設函式f(x)在區間[...
歐拉韁繩理論是由歐拉發現的一條力學規律。起源 18世紀,著名的數學家歐拉曾經研究過摩擦力跟繩索繞在柱子上的圈數之間的關係。得出了著名的“歐拉韁繩理論”理論公式 F=fe 公式解釋 在這個公式里,f代表我們所用的力,F代表我們所要...
級數1 − 2 + 3 − 4 + …與格蘭迪級數1 − 1 + 1 − 1 + …聯繫緊密。歐拉將這兩個級數當作1 − 2 + 3 − 4 + …的特例(其中n為任意自然數),這個級數既直接擴展了他在巴塞爾問題上所做的工作,同時也...
,其中 C=0.577 215... 是歐拉常數,。這是歐拉於1740 年發現的,更一般地,級數 稱為廣義調和級數,亦簡稱調和級數,它的通俗名稱是 p 級數,當 p>1 時收斂,p 定義 定義1:正整數的倒數組成的數列,稱為調和數列。定義2:...
歐拉的方法是從正弦函式的泰勒級數展開式開始: 兩邊除以 ,得:現在,的根出現在 ,其中 我們假設可以把這個無窮級數表示為線性因子的乘積,就像把多項式因式分解一樣,如果把這個乘積展開,並把所有 的項收集在一起,我們可以看到,的...
歐拉函式的展開式如下: 即 歐拉函式展開後,有些次方項被消去,只留下次方項為1, 2, 5, 7, 12, ...的項次,留下來的次方恰為廣義五邊形數。若將上式視為冪級數,其收斂半徑為1,不過若只是當作形式冪級數來考慮,就不會...
如歐拉常數、歐拉恆等式、歐拉級數、歐拉積分、歐拉微分方程、歐拉準則、歐拉變換、歐拉坐標、歐拉求積公式、歐拉方程、歐拉剛體運動方程,歐拉流體力學方程等。歐拉有堅忍的毅力和勤奮刻苦的拼搏精神。他28歲時,為計算彗星的軌跡,奮戰三天三...
自然常數,符號e,為數學中一個常數,是一個無限不循環小數,且為超越數,其值約為2.718281828459045。它是自然對數函式的底數。有時稱它為歐拉數(Euler number),以瑞士數學家歐拉命名;也有個較鮮見的名字納皮爾常數,以紀念蘇格蘭...
可和到1/2。大部分可和法與相應冪級數的解析延拓相關,每個適當的可和法試圖描述的是序列趨於無窮時的平均表現,這種意義下也可以理解為無窮序列的均值。發展歷史 19世紀前,歐拉以及其他數學家廣泛地套用發散級數,但經常引出令人困惑與...
展開並逐項積分,得到了自然對數的無窮級數。“自然對數”最早描述見於尼古拉斯·麥卡托在1668年出版的著作《Logarithmotechnia》中,他也獨立發現了同樣的級數,即自然對數的麥卡托級數。大約1730年,歐拉定義互為逆函式的指數函式和自然對數...
級數表示法 函式li(x)與指數積分Ei(x)有以下的關係:其中x>1。這個等式提供了li(x)的一個級數表示法:其中γ ≈ 0.57721 56649 01532 ...是歐拉-馬歇羅尼常數。一個收斂得更快的級數,是:漸近展開式 當x→ ∞,函式有以下...
Rn就是著名的拉格朗日餘項形式.他還著重指出,泰勒級數不考慮餘項是不能用的.雖然他還沒有考慮收斂性,甚至各階導數的存在性,但他強調Rn要趨於零.表明他已注意到收 題.他同歐拉、達朗貝爾等在任意函式能否表為三角級數的長期爭論,...
