歐拉變換是利用級數項的差分重組級數的方法,把級數進行變換,變換級數的過程和方法稱為歐拉變換。
基本介紹
- 中文名:歐拉變換
- 外文名:Euler transformation
- 適用範圍:數理科學
簡介



性質






套用




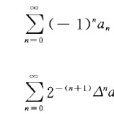
歐拉變換是利用級數項的差分重組級數的方法,把級數進行變換,變換級數的過程和方法稱為歐拉變換。













歐拉變換是利用級數項的差分重組級數的方法,把級數進行變換,變換級數的過程和方法稱為歐拉變換。簡介歐拉變換是利用級數項的差分重組級數的方法,把級數變換為級數的過程和方法稱為歐拉變換。其中。性質當級數收斂時,級數也收斂,且有...
如今幾乎每一個數學領域都可以看到歐拉的名字,從初等幾何的歐拉線、多面體的歐拉定理、立體解析幾何的歐拉變換公式、四次方程的歐拉解法,到數論中的歐拉函式、微分方程的歐拉方程、級數論的歐拉常數、變分學的歐拉方程、複變函數的歐拉公式...
重複一系列可以簡化網路卻不改變其歐拉數(也是歐拉示性數)的額外變換。若有一個多邊形面有3條邊以上,我們劃一個對角線。這增加一條邊和一個面。繼續增加邊直到所有面都是三角形。除掉只有一條邊和外部相鄰的三角形。這把邊和面的...
實定向偶維向量叢上的歐拉示性類 歐拉示性類與龐特里亞金示性類的比較(k=2r)龐特里亞金示性類是不變多項式,無論用黎曼聯絡或者用一般線性聯絡都是在群的變換下不變的,二者所得上同調類相等。歐拉類則只在黎曼聯絡SO(k)變換下...
的歐拉變換便可定義為:用現代術語來說,1 − 2 + 3 − 4 + …是歐拉可求和並為⁄₄。歐拉可求和也包含有另一種可求和法。將1 − 2 + 3 − 4 + …表示為:就有了相關的處處收斂級數:因此 1 − 2 + 3 ...
如歐拉常數、歐拉恆等式、歐拉級數、歐拉積分、歐拉微分方程、歐拉準則、歐拉變換、歐拉坐標、歐拉求積公式、歐拉方程、歐拉剛體運動方程,歐拉流體力學方程等。歐拉有堅忍的毅力和勤奮刻苦的拼搏精神。他28歲時,為計算彗星的軌跡,奮戰三天三...
雷射線掃描感測器安裝於機器人末端法蘭盤上,且設定雷射線掃描感測器坐標系(簡稱感測器坐標系)與機器人基坐標系平行,感測器坐標系及機器人基坐標系均符合右手法則,本例中機器人基坐標系都符合右手法則,由於機器人的運動姿態遵循歐拉變換...
第三章闡述機器人運動方程的表示與求解,包括機械手運動姿態、方向角、運動位置和坐標的運動方程以及連桿變換短陣的表示,歐拉變換、滾?仰?偏變換和球面變換等求解方法,機器人微分運動及其雅可比矩陣等。第四章涉及機器人動力學方程、動態...
歐拉定理揭示了簡單多面體的頂點數、面數、棱數存在著的關係:V+F-E = 2。常數2是簡單多面體經過拓撲變換下的不變數。它是一個與通常的長度、角度、面積、體積等度量無關的數。歐拉定理(或歐拉公式)是拓撲學中的一個重要公式,在...
歐拉在解析延拓被定義前普遍地套用這個概念,並且給出了冪級數解析延拓的精確形式。歐拉變換的操作能被重複上好幾次,它本質上等價於考慮冪級數在z=1處的解析延拓。狄利克雷級數的解析延拓 考慮狄利克雷級數 解析延拓到s=0處的值,...
L.歐拉在化三元二次型到主軸的著作里隱含出現了特徵方程概念,J.L.拉格朗日為處理六大行星運動的微分方程組首先明確給出特徵方程概念。特徵方程也稱永年方程,特徵值也稱本徵值、固有值。固有值問題在物理學許多部門是重要問題。線性變換或...
利用雷諾輸運方程及積分變換,可以得到下面的方程成立:上式即以應力表示的歐拉型微分形式的動量方程。若結合本構方程可得Navier-Stokes方程即N-S方程。3)能量方程 根據能量守恆定律,單位時間內由外界傳入的熱量與外力對系統所作的功之和...
3.2坐標變換 3.3齊次坐標和齊次變換 3.3.1齊次坐標 3.3.2齊次變換 3.4齊次變換矩陣的運算 3.5機器人常用坐標系及變換方程 3.6歐拉變換與RPY變換 3.6.1歐拉角與歐拉變換 3.6.2RPY角與RPY變換 3.6.3機械手歐拉腕和RPY腕...
4.2 歐拉變換解 4.3 PuMA560逆運動學 習題 第5章 速度與靜力學關係 5.1 速度的符號表示 5.2 剛體的線速度和角速度 5.3 機器人連桿間速度傳遞 5.4 機器人雅可比矩陣 5.5 機器人靜力關係 習題 第6章 機...
黎曼不變數是在守恆方程系統上進行的數學變換,使它們更容易得解。在得偏微分方程特徵曲線上,黎曼不變數是常數。最初是由伯恩哈德黎曼在研究氣體動力學中的平面波工作中提出的。先寫一組一維歐拉方程:其中,可以是守恆變數也可以是原始...
自然常數,符號e,為數學中一個常數,是一個無限不循環小數,且為超越數,其值約為2.718281828459045。它是自然對數函式的底數。有時稱它為歐拉數(Euler number),以瑞士數學家歐拉命名;也有個較鮮見的名字納皮爾常數,以紀念蘇格蘭...
歐拉、拉格朗日、高斯、泊松和拉普拉斯等許多著名的學者都為它的發展作過不少貢獻,先後提出過的攝動方法不下百種。歸納起來,大致可分三類:坐標攝動法、瞬時橢圓法和正則變換法。有些方法不能明確地列入哪一類,例如著名的漢森方法就兼...
3.1.3 連桿變換矩陣及其乘積 3.2 機械手運動方程的求解 3.2.1 歐拉變換解 3.2.2 滾、仰、偏變換解 3.2.3 球面變換解 3.3 PUMA560機器人運動方程 3.3.1 PUMA560運動分析 3.3.2 PUMA560動綜合 3.4 小結 習題 第4...
法國數學家傅立葉認為,任何周期函式都可以用正弦函式和餘弦函式構成的無窮級數來表示(選擇正弦函式與餘弦函式作為基函式是因為它們是正交的),後世稱傅立葉級數為一種特殊的三角級數,根據歐拉公式,三角函式又能化成指數形式,也稱傅立...
