發散性
級數項(1, −2, 3, −4, …)沒有趨近於
0;因此可通過
項測試來確定1 − 2 + 3 − 4 + …發散。作為後文的參考,此方法也常被用於從基礎級上預見發散。從定義可知,無窮級數的收斂或發散是由其部分和的收斂或發散確定的,1 − 2 + 3 − 4 + …的部分和為:
此部分和序列的一個顯著特點是每個整數都出現了一次——如果將空部分和計入還包括0——因此其
可數集為整數集。很明顯的,不可能讓變化的結果收斂到一個確定的數,因此1 − 2 + 3 − 4 + …發散。
求和的啟發
穩定性與線性
由於各項 1, −2, 3, −4, 5, −6, … 以一種簡單模式排列,級數1 − 2 + 3 − 4 + …可表示為它自己的變換形式(概略的說法),而因此所得的方程解取得一數值。暫時假設寫作s = 1 − 2 + 3 − 4 + …有意義——其中的s為常數,然後再處理的問題:
因此,,如右圖所示。
複製4份 1 − 2 + 3 − 4 + …,僅使用移動與項項相加,結果為1。左右兩邊的兩個1 − 2 + 3 − 4 + …副本相互抵消,並得出1 − 1 + 1 − 1 + …。
儘管1 − 2 + 3 − 4 + …沒有通常意義的和,等式
s = 1 − 2 + 3 − 4 + … =卻可被賦予另外一種意義。離散級數之“和”的一種
普遍定義被稱為一種求和法或可和法——對所有可能級數的一些子集求和。有許多種不同的方法(部分將在
下文中出現),這些方法有著與常數求和所共有的特性。以上的處理實際上都可由下述所證明:給出任意的線形且穩定的可和法,並計算級數1 − 2 + 3 − 4 + …,結果為此外,由於:
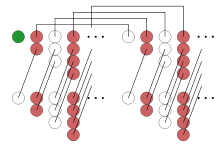 複製4份
複製4份柯西乘積
1891年,
恩納斯托·切薩羅發表了將
發散級數嚴密地帶入
微積分學的想法,並指出:“已可寫出(1 − 1 + 1 − 1 + …) = 1 − 2 + 3 − 4 + …並斷定兩邊均等於。”對切薩羅而言,這個等式是他前幾年發表的一個定理的套用,該定理也許是歷史上可求和的發散級數的第一個定理。關於此求和法的詳細內容請見
下文;其中心思想是1 − 2 + 3 − 4 + …是1 − 1 + 1 − 1 + …對1 − 1 + 1 − 1 + …的
柯西乘積。
1 − 2 + 3 − 4 + … 以 1 − 1 + 1 − 1 + … 的二重柯西乘積出現

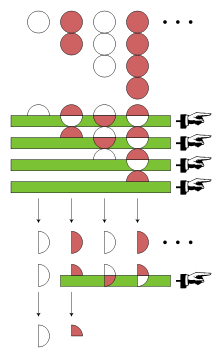
兩個無窮級數的柯西乘積可被確定,即使在他們都發散的時候。在 Σan= Σbn= Σ(−1) 的情況下,柯西乘積的項可由有窮對角線求和的方式給出:
積級數為:
這樣一種考慮到兩個級數的柯西乘積與結果的求和法,也能夠求出。由前部分的結果可知,當方法是線形、穩定並考慮到柯西乘積的時候,1 − 1 + 1 − 1 + …與1 − 2 + 3 − 4 + …的可求和之間是等價的。
切薩羅的定理是一個深奧的例子。級數1 − 1 + 1 − 1 + …在最弱的意義上是切薩羅可求和,稱作(C, 1)-可求和,然而1 − 2 + 3 − 4 + …則需要切薩羅的定理的一個更強的形式,表示為(C, 2)-可求和。由於切薩羅的定理的所有形式均為線形且穩定的,所得的值正是此前計算所得的。
特殊方法
切薩羅與赫爾德
關於⁄4的(H, 2)和的數據
若1 − 2 + 3 − 4 + …的(C, 1)切薩羅和存在,要找到其數值就需要計算該級數部分和的
算術平均值。 部分和為:

這些部分和的算術平均值為:
此平均值序列沒有收斂,因此 1 − 2 + 3 − 4 + … 不是切薩羅可求和。
切薩羅求和有兩種有名的廣義化:讓這些在概念上更簡單的是(H,
n)法的序列,其中
n為
自然數。(H, 1)和為切薩羅求和,更高的方法則重複平均值的計算。在上文中,偶數平均值趨近於⁄
2,奇數平均值則全部等於0,所以平均值
的平均值趨近於 0 與⁄
2的平均數,即⁄
4。因此,1 − 2 + 3 − 4 + …是(H, 2)-可求和為⁄
4。
符號“H”代表奧圖·赫爾德。
1882年,他第一次證明了被現在數學家們所看作的在阿貝耳求和與(H,
n)求和之間的關係;1 − 2 + 3 − 4 + …是第一個例子。⁄
4是1 − 2 + 3 − 4 + …的(H, 2)和這個事實也保證了它是阿貝耳和;這些都將在下文直接予以證明。
另外一個普遍明確的切薩羅求和的廣義化,是(C,
n)法的序列。已經證明了(C,
n)求和與(H,
n)求和均能給出相同的結果,但是它們卻有不同的歷史背景。在
1887年,切薩羅已經接近於陳述出(C,
n)求和的定義了,但是他只給出了少量的例子。特別的,他在計算1 − 2 + 3 − 4 + …,為⁄
4時所採用的方法可能是(C,
n)的另一種描述,但是在當時並沒有對其進行證明。他在1890年正式定義了(C, n)法,以陳述他的定理:一個(C,
n)-可求和級數與一個(C,
m)-可求和級數的柯西乘積是(C,
m +
n + 1)-可求和。
阿貝耳求和
1−2x+3x+…; 1/(1 + x) 的一部分;其極限為1
……當該級數1 − 2 + 3 − 4 + 5 − 6 …的和為⁄4時,那肯定出現了悖論。對該級數的100項相加,我們得到了-50,但是,101項的和卻給出+51,這與⁄4是截然不同的,而且這種差距還會隨著項數增加而變得更大。不過我在前一段時間已經注意到了,有必要給“和”這個詞賦予一個更加廣泛的意義……。
歐拉曾幾次提議將“和”這個詞廣義化。在1 − 2 + 3 − 4 + …,的情況下,他的構想與現在所知的阿貝耳求和相似:
……毫無疑問,級數1 − 2 + 3 − 4 + 5 + …的和為⁄4;由於它是由公式⁄(1+1)展開而成,而此公式的值明顯為⁄4。在考慮一般級數1 − 2x + 3x − 4x + 5x− 6x + …後這個概念變得更明晰了。這個一般級數是由表達式⁄(1+x)展開而成,當我們讓 x = 1 後,這個級數就確確實實地相等了。
在當
絕對值 |
x| < 1 時,有許多方式去驗證歐拉的下列等式正確:
可以將泰勒展開式的右邊拿掉,或使用正規的多項式長除。從左方開始,可採用上文的一般啟發式並嘗試乘以兩次(1+
x),或對幾何級數1 −
x +
x − …求平方。歐拉似乎也提出可以對後者級數的每項求
微分。
以現代的眼光看,級數 1 − 2
x + 3
x − 4
x + … 並沒有定義一個在
x = 1時的
函式,因此其值不能簡單地被替換為結果表達式。由於函式被定義為滿足所有的|
x| < 1,所以仍可取得
x趨近於1的極限,而這就是阿貝耳和的定義:
歐拉與波萊爾
⁄2−⁄4的歐拉求和
歐拉對該級數還使用了另外一種技巧:
歐拉變換,這是他自己的發明。要計算歐拉變換,首先要有可形成交錯級數的正項序列——在此情況下為1, 2, 3, 4, …。將此序列中的首項標示為
a0。
下一步需要1, 2, 3, 4, …的
前向差分;這恰好是1, 1, 1, 1, …。將該序列的首項標示為 Δ
a0。歐拉變換也基於差分的差分,以及更高的疊函式,但是1, 1, 1, 1, …的前向差分為0。1 − 2 + 3 − 4 + …的歐拉變換便可定義為:
用現代術語來說,1 − 2 + 3 − 4 + …是歐拉可求和並為⁄4。
歐拉可求和也包含有另一種可求和法。將1 − 2 + 3 − 4 + …表示為:
就有了相關的處處收斂級數:
因此 1 − 2 + 3 − 4 + … 的波萊爾和為:
比例分離
賽切夫與Woyczyński只通過兩個物理原理便得出了1 − 2 + 3 − 4 + … =⁄
4,這兩個原理分別是:無窮小鬆弛(
infinitesimal relaxation)與比例分離(
separation of scales)。為了表示得精確,他們為這些原理定義了一系列的“
φ-求和法”,所有這些方法都可以將級數求和得⁄
4:
該結果推廣了阿貝耳求和,當取
φ(
x) = exp(−
x)時可得到先前的等式。此一般陳述可通過將關於
m的級數中的項配對,並將表達式變換為
黎曼積分的形式予以證明。在後一步中,對1 − 1 + 1 − 1 + …的相應證明運用了
中值定理,但在這裡需要
泰勒公式中更強的拉格朗日形式。
廣義化
1755年的《Institutiones》上,歐拉對相似的級數求和
1 − 1 + 1 − 1 + …的三倍柯西乘積為1 − 3 + 6 − 10 + …,為
三角形數的交錯級數;其阿貝耳與歐拉和為⁄
8。1 − 1 + 1 − 1 + …的四倍柯西乘積為1 − 4 + 10 − 20 + …,為
四面體數的交錯級數,這個的阿貝耳和為⁄
16。
另一個1 − 2 + 3 − 4 + …在略微不同的方向的廣義化是級數1 − 2 + 3 − 4 + …,使用了另外的值n。對正整數n來說,此級數有下列的阿貝耳和:
其中,n為正數。這是一個笑料,朋友。”
切薩羅的老師歐仁·查理·卡塔蘭也輕視發散級數。在卡塔蘭的影響下,切薩羅早期提出1 − 2 + 3 − 4 + …的“習用式”是“荒謬的等式”;而在
1883年,切薩羅表明了當時的一個典型看法:公式是錯的,不過在某些場合在形式上是有用的。最後,在他
1890年的書《
Sur la multiplication des séries》中,切薩羅使用了一個接近於定義的模型。
此級數亦研究過
n為非線性值的情況;這產生了狄利克雷η函式。歐拉研究1 − 2 + 3 − 4 + …相關級數的部分動機是η函式的泛函方程,這直接導向了
黎曼ζ函式的泛函方程。歐拉在正偶整數(包括在
巴塞爾問題中)時找到這些函式值的建樹已讓他聞名世界,他也試圖找到正奇整數(包括在
阿培里常數中)時的值,但這個問題直到今天都是令人困惑的。η函式通過歐拉的方法解決會更加簡單,因為它的
狄利克雷級數是處處阿貝耳可求和;η函式的狄利克雷級數非常難以對發散的部分求和。例如,1 − 2 + 3 − 4 + …在η函式中的相似級數是非交錯級數1 + 2 + 3 + 4 + …,該級數在現代
物理學上有很深的套用,不過需要非常強的方法才能求和。




 複製4份
複製4份
