基本介紹
- 中文名:極限集
- 外文名:limit set
- 所屬領域:動力系統
- 分類:ω極限集或α極限集
- 性質:動力系統研究的基本對象
定義












相關性質定理



























例題分析







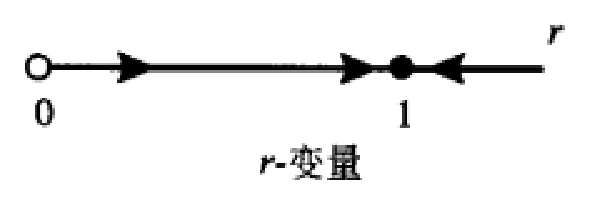
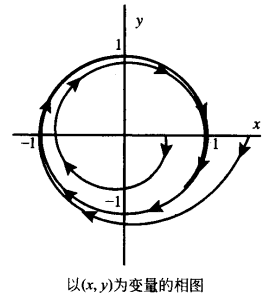



































































極限集(limit set)是動力系統由極限點組成的集合。極限點指隨著時間向正負兩個方向趨於無窮時該點所在的軌道會無窮次接近它的點。如果只考慮時間趨於正或負無窮,則可分別得到ω極限集或α極限集。極限集是動力系統研究的基本...
由上述定義易見,奇點x0是φτ(x0)=x0的惟一的ω和α極限點,閉軌φτ(x0)上的任一點都是此閉軌的ω和α極限點。亦即,奇點和閉軌分別為它們自身的ω和α極限集。 對於平面定常系統 ,極限集理論有甚為清晰完整的結論,可歸結如下...
α極限集合 α極限集合(α-limit set)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
數列上極限 給定無窮數列 ,它的一切收斂子數列的極限值的上確界值,稱為該無窮序列的上極限。或定義為 。因為 是遞減的,所以討論其極限值是有意義的。集合上極限 給定無窮集合列 , 稱為無窮集合列的上極限集,含義為屬於...
在數學中,特別是在動態系統理論里,一個二維平面或二維流形上的的極限環是相空間裡的一個閉合的軌跡。若系統在其極限環Γ外側(內側)足夠小鄰域內的軌線均以Γ為Ω極限集,則稱Γ為外(內)穩定極限環。簡介 在數學中,特別是在動態...
a極限點 (a-limit point)動態系統隨時間倒退而趨近的極限點.具體說來,動態系統經過點x 而令時間t減小所得的相軌稱為負半軌,並記為 O} (x).負半軌的極限點稱為x的a極限點,極限點的集合記為a(x),稱為x的a極限集.
則可以有結構複雜的極限集,例如混沌集等。基本介紹 定理 (龐加萊-本迪克松定理) 考慮 上的微分方程 。(a)假設 在 上有定義,正半軌 有界,則 :(i)含有不動點或(ii)是周期軌。(b)假設 是有界閉子集且是微分方程的正不變集...
極限行為 通過疊代,可以發現有向一個單一點收縮和會聚的一個集合。在這種情況下,會聚到的這個點叫做吸引不動點。反過來說,疊代也可以表現得從一個單一點發散;這種情況叫不穩定不動點。當軌道的點會聚於一個或多個極限的時候,...
1.1.2 積集,商集,極限集 1.1.3 Cantor定理與Zorn引理 1.2 拓撲空間 1.2.1 拓撲空間的基本概念 1.2.2 可數性公理及分離性公理 1.2.3 緊性與連通性 1.3 測度空間 1.3.1 可測空間與可測映射 1.3.2 實值函式與...
極限集為x),另一為P一穩定(其a極限集為x).對於半流和離散半動力系統只有P穩定軌道.泊松穩定軌道有時又稱為回復軌道,特別是在離散情形,這種稱謂更為多見(參見“回復軌道”).泊松穩定軌道是龐加萊(Poincare, (J.-)H. )於1899...
極限集與 極限集均為臨界元素;2. 所有臨界元素是雙曲的;3. 無鞍點間的連線軌道。定理3 (Peixoto)設M為緊緻 二維可定向流形(),若且唯若 是M-S向量場時,為結構穩定。定理4 (帕利斯-斯梅爾)每一微分同胚 是 結構穩定的,每...
極限集和a極限集都只能是奇點或周期軌道,但它們不同時都是鞍點.佩克索托定理是佩克索托(Peixoto , M.)於1962年得到的.佩克索托為了證明上述定理,還給出C'稠密性定理,即:閉曲面上所有結構穩定系統在其上的全體C'向量場空間中作成一...
5.4極限集 5.5梯度系統 5.6套用 5.6.1非線性振子 5.6.2神經網路 5.7理論與證明 練習 第6章周期軌 6.1定義與例題 6.2龐加萊本迪克松定理 6.3自激振子 6.4安德羅諾夫霍普夫分支 6.5周期軌的同宿分支 6.6流作用下面積...
《分段光滑系統的分支問題》是依託華僑大學,由皮定恆擔任項目負責人的青年科學基金項目。項目摘要 Buzzi等學者在2010年證明了一類分段光滑系統的雙曲鴨環是雙曲極限環的極限集.他們對該分段光滑系統使用正則化過程和blow up 技巧得到了一...
建立離散Lyapunov 泛函作用與嵌套k秩錐簇存在性的等價關係,並考察嵌套錐簇關於斜積半流光滑擾動的保持,進而研究離散Lyapunov 泛函作用下的斜積半流極小集(及極限集)的提升性質,維數嵌入性質及其相應的C1-擾動結構穩定性。利用此統一...
處的不穩定集、(尺度為ε的)局部穩定集和局部不穩定集。記 為φ過點 的軌道,集合 分別稱為φ的過點 軌道的穩定集和不穩定集。顯然,若 是同胚 (連續流φ)的不動點,則 與 與 分別是由以 為ω極限集和以 ...
2.2 軌線的極限集合 2.3 平面上的極限集 2.4 極限集的套用實例 習題2 第三章 穩定性理論 3.1 穩定性的定義和例子 3.2 自治系統零解的穩定性 3.3 非自治系統的穩定性 3.4 全局穩定性 3.5 線性系統及其擾動系統的穩定性...
人們用(i,j)表示長方形E(i,j)),從而R₀亦表示經映射S,i,j∈R₀所得的長方形族。令𝓘=∪S,則𝓘(E₀)= 重複上述過程,而將每一E(i,j)用𝓘(E(i,j))代替,最後得到的極限集 即為麥克繆倫集。
A22平衡點、不變集、極限集 209 A23非線性自治系統在平衡點處的線性化處理 210 A3穩定性的基本概念 212 A31自治系統零解的穩定性 213 A32線性系統的穩定性 214 A4非線性動力系統的穩定域理論 216 A41自治系統平衡點的分類 216 A42...
對於非線項具有反射對稱性的特殊情形,對極限集結構做系統深入刻劃。對於圓周上一般情形的幾乎周期驅動反應擴散方程深入研究新幾乎自守現象的存在性以及幾乎周期驅動圓周流的存在性。 結題摘要 播報 編輯 本項目主要研究了一維周期邊條標量非...
我們證明了一族三維自仿tile與球同胚;證明了一大類二維自相似tile為擬圓盤,且一般自仿tile為非擬圓盤;求出了一類廣義有限型測度的Lq譜,並證明其可導性;研究了無窮有重疊疊代函式系並證明了通過拓撲熵求極限集維數的公式;得出了有...
非遊蕩集(nonwandering set)是動力系統中的重要的不變集。一個動力系統f的所有非遊蕩點的集合稱為f的非遊蕩集,記為Ω(f)。對於緊空間上的動力系統,非遊蕩集是非空的閉不變集,而且由於極限集屬於非遊蕩集,因此所有的軌道,當時刻...
在右端函式次線性的條件下,討論拉回軌線極限集的分類。接著,研究由Brown運動驅動的隨機泛函微分方程(SFDE),尋求擴散項的條件,使得SFDE與某些RFDE可測共軛,由此獲得其解生成RDS、強序保持、次線性的條件,並獲得吸引子、平穩解、...
第一章 集論 1 集的運算 1.集合的概念 2.子集·冪集·差集 3.並集·交集·乘集 4.集的運算 5.極限集 6.Peano自然公理 7.習題 2 映照 1.映照的概念 2.逆映射·複合映射·映射的限制和延拓 3.集的剖分 4.特徵函式·簡單...
《C*上復動力系統》是依託北京理工大學,由方麗萍擔任項目負責人的青年科學基金項目。項目摘要 本項目首先研究了c(*)上全純自映射f的Sulia集J(F)與奇點極限集Io(f)和I∞(f)的關係,證明了J(f)=2Io(f)=2I∞(f),並且J(...
