基本介紹
一些數據
- 1, 2, 3, ...:
- 1, 2, ...
- 1, 1, 2, 3, 4, 5 ...
- 1, 1, 2, ...
- 維數 − 修正項 = 度數 −g+ 1。
定理的陳述
- l(D) −l(K−D) =deg(D) −g+ 1.
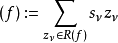
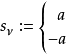 | ,如果 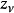 |
,如果 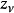 |
- l(K−D) ≥ 0,
- l(D) ≥deg(D) −g+ 1
- 1, 1,?, 2, 3, ... .

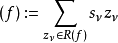
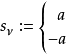 | ,如果 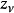 |
,如果 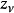 |
黎曼–羅赫定理(Riemann–Roch theorem)是數學中,特別是複分析和代數幾何,一個重要工具,它可計算具有指定零點與極點的亞純函式空間的維數。它將具有純拓撲虧格 g...
他研究了阿貝爾函式和阿貝爾積分及阿貝爾積分的反演,得到著名的黎曼—羅赫定理,首創的雙有理變換構成19世紀後期發展起來的代數幾何的主要內容。...
其中對黎曼曲面從拓撲、分析、代數幾何各角度作了深入研究。創造了一系列對代數拓撲發展影響深遠的概念,闡明了後來為G.羅赫所補足的黎曼-羅赫定理。1857年,升為...
龐加萊((J.-)H.Poincaré)具體構造Θ級數,後稱為龐加萊級數,以此證明對給定的G是自守的函式的存在,閉黎曼曲面的一個重要定理是黎曼-羅赫定理,它給出閉黎曼...
黎曼-羅赫定理給出閉黎曼曲面上亞純函式構成的線性空間的維數,兩黎曼曲面,如果存在映一個為另一個的共形映射,則稱它們是共形等價的。...
龐加萊((J.-)H.Poincaré)具體構造Θ級數,後稱為龐加萊級數,以此證明對給定的G是自守的函式的存在,閉黎曼曲面的一個重要定理是黎曼-羅赫定理,它給出閉黎曼...
龐加萊((J.-)H.Poincaré)具體構造Θ級數,後稱為龐加萊級數,以此證明對給定的G是自守的函式的存在,閉黎曼曲面的一個重要定理是黎曼-羅赫定理,它給出閉黎曼...
在數學中,黎曼曲面是德國數學家黎曼為了給多值解析函式構想一個單值的定義域而...黎曼-羅赫定理稱:在一個虧格為g的閉曲面上,指定了點p1,p2,…,ps;q1,q2,...
該定理斷言,對於緊的可定向的流形上的線性橢圓微分運算元,其解析指標等於拓撲指標。 [2] [5] 幾何和拓撲學中的許多大定理,包括黎曼-羅赫定理(Riemann-Roch Theore...
把指標定理套用於鐸爾博爾復形就得出黎曼-羅赫-希策布魯赫定理(Riemann-Roch-Hirzebruch therorem)。...
約翰·查爾斯·菲爾茲,1863年5月14日生於加拿大渥太華,著名數學家。1906年,證明了黎曼一羅赫定理。...
來到巴黎南部建於1958年的IHES研究所,他美妙的格羅滕迪克-黎曼-羅赫定理開始引起了人們對他的注意,接著是一系列高產的討論班。格羅滕迪克本人實際上沒有走在...
閉黎曼曲面k上的亞純微分稱為阿貝爾微分。阿貝爾微分分為第一類阿貝爾微、第二類...。關於這些空間的維數的另一重要信息包含在黎曼-羅赫定理中:等式對...
1954年,他表述並證明了代數簇的黎曼一羅赫定理,得到的公式稱為希策布魯赫一黎曼一羅赫公式。1959年,他與阿蒂亞(Atiyah , M. F.)合作引人了K理論。他們根據格...
來到巴黎南部建於1958年的IHES研究所,他美妙的格羅滕迪克-黎曼-羅赫定理開始引起了人們對他的注意,接著是一系列高產的討論班。格羅滕迪克本人實際上沒有走在...
諾特、 H.哈塞、F.K.施密特和 A.韋伊以及其他學者的逐步簡化和推廣,對域F的限制得以逐步解除,使這一理論的許多內容包括黎曼-羅赫定理,可以在F為任意域的情況...
Ⅴ.31黎曼羅赫定理Ⅴ.32Robertson—Seymour定理Ⅴ.33三體問題Ⅴ.34單值化定理Ⅴ.35韋伊猜想第Ⅵ部分數學家傳記Ⅵ.1畢達哥拉斯Ⅵ.2歐幾里得...
這裡用來代表黎曼曲面等價類參數,稱為它的模(modulus)。由黎曼曲面的黎曼-羅赫定理可以推出,虧格為零的緊黎曼曲面必然共形等價於黎曼球面。因此, 中只有一個元素...
