基本介紹
- 中文名:典範除子
- 外文名:canonical divisor
- 所屬學科:數學
- 所屬問題:代數幾何
- 性質:代數簇上的一類特殊的除子
基本介紹
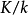
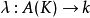
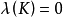
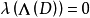
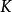
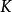
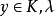
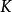
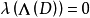
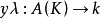
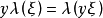
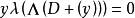
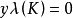
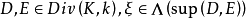
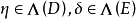
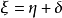

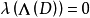
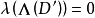
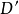
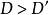
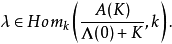
相關定理
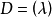
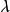
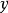
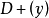
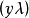
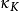
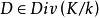
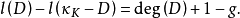
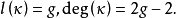

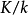
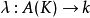
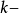
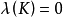
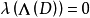
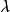
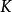
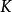
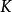
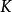
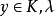
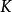
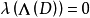
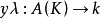
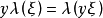
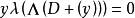
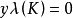
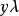
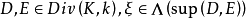
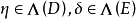
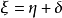
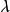

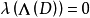
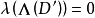
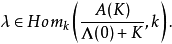
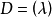
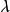
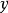
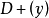
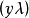
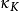
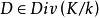
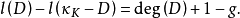
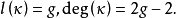
典範除子(canonical divisor)是代數簇上的一類特殊的除子。具體地,若X是光滑代數簇,ΩX1是X上的正則1形式芽層,ωX=∧rΩX1,r=dim X,則稱可逆層ωX對應的...
這裡ω_{X/C}是相對典範層, ω_{X/C}·ω_{X/C} 是相對典範除子的自交數(就是和自身的相交數)。如果f不是半穩定纖維化, 那么不等式需要修改為:...
典範映射是代數幾何中最基本的概念之一。 由典範除子的線性系定義的有理映射,叫做典範映射。 每個代數簇都自帶了典範除子,所以典範映射本質地反映了這個代數簇的...
一個整體亞純函式的除子叫做主除子。相差一個主除子的兩個除子稱為線性等價。一個整體亞純 1-形式的除子叫做典範除子(通常記作K)。任何兩個亞純 1-形式...
設C是代數曲線, D是C上的除子,K是C上的典範除子,g是C的虧格。我們記上同調h^0(D)=dim |D| -1, 其中|D|是D的完全線性系,它是一個射影空間, dim...
主要從事代數曲面的研究工作。 在代數曲面的纖維化, 高次典範除子, 曲面自同構群等方面有著傑出的貢獻。肖剛的學生中有:陳猛、蔡金星、談勝利、孫笑濤等國內傑出...
主要從事代數曲面的研究工作。 在代數曲面的纖維化, 高次典範除子, 曲面自同構群等方面有著傑出的貢獻。肖剛的學生中有:陳猛、蔡金星、談勝利、孫笑濤等國內傑出...
人們主要藉助於由典範除子誘導的典範映射以及多重典範映射 的性質來刻畫和分類一般型極小曲面。在很多情形下,有帶維化結構的一般型曲面也常常能夠通過其纖維結構來...
克利福德定理(Clifford's theorem)給出代數曲線上的特殊除子的維數上界的定理.設D是光滑射影曲線C上的一個除子,若h0(D) = L(D)筍。,hl(D) = L(K一D...
然後可定義極小模型為:典範除子為半正的、僅含末端奇點的射影簇.極小模型猜想認為小平維數非負的光滑射影簇必有極小模型.在三維的情形這個猜想已被森重文證明...
