部分分式分解(partial fraction decomposition) 亞純函式在極點處的一種表示式。
基本介紹
- 中文名:部分分式分解
- 外文名:Partial fraction decomposition
- 適用領域:數學
定義
- 分式的分子多項式次數需比其分母多項式次數要低。
例子




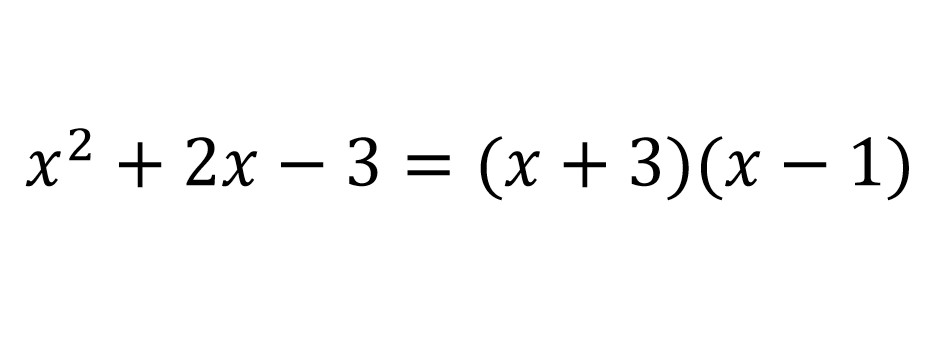



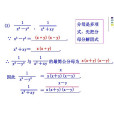
部分分式分解(partial fraction decomposition) 亞純函式在極點處的一種表示式。




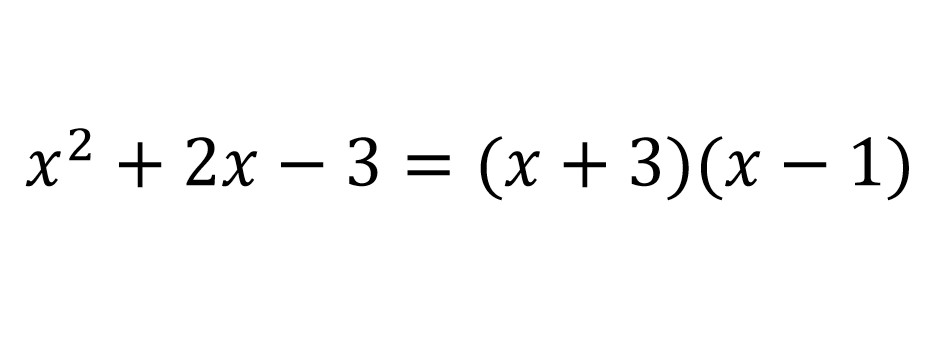



部分分式分解(partial fraction decomposition) 亞純函式在極點處的一種表示式。定義部分分式分解或部分分式展開,是將有理函式分解成許多次數較低有理函式和的形式,來降低分子或分母多項式的次數。分...
部分分式是一種特殊形式的分式,即把數域 F 上的分式 f(x)/g(x) 分解成分式的和時,部分分式是指如下形式的項 其中 p(x) 是數域 F 上的不可約多項式,m 是自然數,r(x) 是 F 上的次數小於 p(x) 的多項式。分解定理 ...
分式的部分分式分解是分式的一種分解方式.把一個既約有理真分式寫成部分分式和的形式的過程。分解方法 稱為分式的部分分式分解.常用的分解方法有以下幾種:1.待定係數法.對既約真分式Q(二)/P(二),首先將分母P(二)分解因式,寫成...
根據代數知識,有理真分式必定可以表示成若干個部分分式之和(稱為部分分式分解),因而問題歸結為求那些部分分式的不定積分。有理函式積分法的具體介紹 設需要求 其中P,Q都是多項式,如果Q的次數大於或等於P的次數,則先用除法分出商...
複平面上的超越亞純函式也有一個部分分式分解定理 , f(z)是以{ak}為極點集的超越亞純函式,設f(z)在極點ak處羅朗展式的主部為,Pk(u)是一個多項式,於是f(z)可表作:中g(z)是整函式,hk(z)是適當選取的多項式。 對於...
本書主要內容有:參數方程,極坐標,坐標的平移與旋轉變換,有理函式的部分分式分解,行列式,複數的歐拉公式,關於任意性、存在性和唯一性(主要包括證明明不等式解集存在性的放大縮小原理),有限與無限,反例與反證法等。所有這些內容在...
t)的拉普拉斯變換F(s),求原函式f(t)的運算為拉普拉斯反變換。其公式為:常用方法 1、部分分式展開法 將X(s)分解為因式 之和,然後利用拉普拉斯變換公式來求它的逆變換。2、留數法 變換公式為:
如果F是代數閉域,那么由於F[x]內的不可約多項式都是一次的,根據部分分式分解的定理,以上的性質成立。而另一方面,假設以上的性質對於域F成立。設p(x)為F[x]內的一個不可約元素。那么有理函式1/p可以寫成多項式函式q與若干個形...
在有理函式的部分分式分解講解中,該書適當作了一些說明。對 冪級數的展開式處理稍作修改。對一些例題進行適當的增減。將“微積分學簡史”作為數字資源。參加第五版編寫工作的老師有:龐學誠,任主編,並負責編寫第一章至第七章。吳畏...
頻響 這些都比脈衝回響不變法的部分分式分解便捷得多,一般,當著眼於濾波器的時域瞬態回響時,採用脈衝回響不變法較好,而其他情況下,對於IIR的設計,大多採用雙線性變換。
1.4 整函式的因子分解定理 2 picard 定理 2.1 bloch 定理 2.2 landau 定理和picard 第一定理 2.3 schottky 定理和picard 第二定理 3 runge 定理亞純函式部分分式分解定理 3.1 兩個預備定理 3.2 runge 定理 3.3 亞純函式的...
4.3.1 部分分式分解法/116 4.3.2 圍線積分法——留數法/120 4.4 連續時間系統的s域分析/122 4.4.1 微分方程的s域分析/123 4.4.2 電路的s域模型及求解/124 4.5 連續系統的系統函式/128 4.5.1 系統函式及其零、極點...
2.2.5 Laurent展開式及留數 2.3 Jensen公式 2.4 部分分式分解 2.4.1 有理函式部分分式分解 2.4.2 餘切函式的分解及套用 第3章 數論中的特殊函式 3.1 Plana求和公式及套用 3.2 Kubert函式及乘積公式 3.2.1 導引...
,要求F(s)為真分式,即分子的最高次小於分母的最高次,否則使用多項式除法將{F(s)分解 終值定理:,要求sF(s)的所有極點都在左半複平面或原點為單極點。由於終值定理無需經過部分分式分解或其他困難的代數就能給出長期的行為,它...
第3章 多項式和因式分解 3.1 多項式 3.2 復係數與實係數多項式的因式分解 3.3 實數域上的因式分解方法選講 3.4 有理函式的部分分式分解 第4章 極坐標和參數方程 4.1 平面上點的極坐標 4.2 曲線的極坐標方程 4.3 極坐標...
第七講 有理函式的部分分式分解 第八講 有理真分式的遞推公式 第九講 三角函式有理式的不定積分 第十講 某些無理函式的不定積分(1)第十一講 某些無理函式的不定積分(2)第十二講 習題課二 02 定積分 定積分是積分學的...
4.3.1部分分式展開法(partial?fraction expansion method)4.3.2留數法(圍線積分法)4.4線性系統復頻域分析法 4.4.1系統微分方程的復頻域解 4.4.2電路的s域模型 4.4.3復頻域阻抗與復頻域導納 4.4.4線性系統復頻域分析法 4...
5.4 因子分解 5.5 不可約性判定標準 5.6 因子分解在有限步下的完成 5.7 對稱函式 5.8 兩個多項式的結式 5.9 結式作為根的對稱函式 5.1 0有理函式的部分分式分解 第6章 域論 6.1 子體,素體 6.2 添加 6.3 單純...
3.7.2部分分式展開 3.7.3利用傅立葉變換性質和常見信號的傅立葉變換對 3.8LTI系統的頻域分析 3.8.1頻率回響 3.8.2信號無失真傳輸 3.8.3理想低通濾波器的回響 3.9希爾伯特變換 3.9.1因果時間函式的傅立葉變換的實部或虛部...
3.4.2 冪級數展開法 3.4.3 部分分式展開法 第4章 離散時間信號分析 4.1 序列的傅立葉變換 4.2 信號的傅立葉變換、拉普拉斯變換與z變換的關係 4.3 離散傅立葉級數(DFS)4.3.1 傅立葉變換在時域和頻域中的對偶規律 4.3....
5.4.1部分分式展開法 5.4.2圍線積分法(留數法)5.5拉普拉斯變換與傅立葉變換的關係 5.6用拉普拉斯變換求解線性系統的回響 5.6.1高階微分方程的復頻域解 5.6.2狀態方程的復頻域解法 5.7連續時間系統的系統函式 5.7.1單輸入...
4.3.2 部分分式展開法 4.3.3 反演積分法 4.4 連續系統的復頻域分析 4.4.1 連續信號的復頻域分解 4.4.2 基本信號e激勵下的零狀態回響 4.4.3 一般信號 f(t)激勵下的零狀態回響 4.5 系統微分方程的復頻域解 4....
