基本介紹
- 中文名:不可約多項式
- 外文名:irreducible polynomial
- 套用:數學
- 本質:代數式
概念
判定
定理1
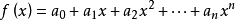
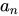
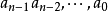
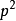
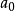
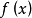
定理2
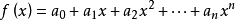
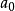
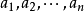
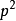
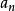
性質
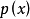
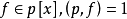
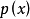
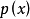
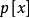
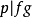
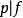
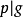
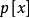
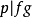
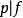
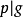
證明
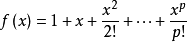
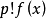
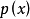
套用
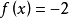
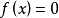
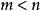
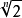
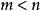

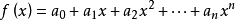
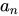
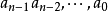
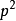
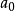
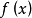
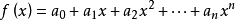
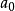
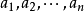
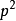
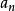
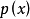
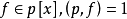
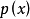
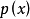
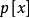
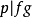
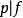
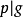
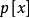
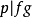
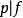
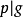
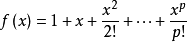
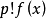
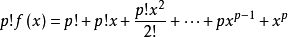
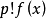
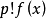
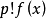
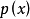
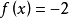
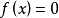
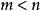
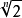
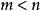
多項式中的每個單項式叫做多項式的項,這些單項式中的最高項次數,就是這個多項式的次數不可約多項式是一種重要的多項式,它在多項式環中有類似於素數在整數環中的地位...
可約多項式(reducible polynomial)一種特殊的多項式.指有非平凡因式的多項式。首先,多項式(polynomial)是指由變數、係數以及它們之間的加、減、乘、冪運算(非負整數...
既約多項式又稱“不可約多項式”。次數大於零的有理數係數多項式,不能分解為兩個次數較低但都大於零的有理數係數多項式的乘積時,稱為有理數範圍內的“既約...
希爾伯特不可約性定理(Hilbert theorem of irreducibility)是判別多元多項式不可約性的一種方法。設f(x1,x2,…,xn)是數域P上的n元多項式,若f在數域P上不可...
不可約元素是抽象代數中的名詞,是指在整環或者非整環中一個非零、非單位的元素,而且也無法表示為二個非單位元素的乘積。結一不可約元素和交一不可約元素統稱...
一類重要的多項式.指既約因式在任意擴域內無重根的多項式.設f(x)是域F上次數大於零的多項式,若f(x)的每個既約因式在F的代數閉包內沒有重根,則稱f(x)為...
F[x]中任一個次數不小於 1的多項式都可以分解為F上的不可約多項式的乘積,而且除去因式的次序以及常數因子外,分解的方法是惟一的。...
不可約線性變換(irreducible linear transfor-mation)亦稱不可分解線性變換一種特殊的線性變換.設V是域P上的n維線性空間,aEHom,}<V,V),若除。,V外,不存在a...
可約的概念滲透到數學的各個分支, 它在不同的分支中有不同的表現形式。與可約概念相對的就是不可約。...
有理係數多項式是高等代數裡面多項式因式分解討論的一個特例。我們知道,每個次數大於等於1的有理係數多項式都能惟一地分解成不可約的有理係數多項式的乘積。但是對於...
多項式分裂域(splitting field of a polynomial )與多項式相關的一種域。 在抽象代數中,具有域中係數的多項式分裂域是該域的最小域延伸,多項式在該域上分裂為線性...
本書分為多項式的根、不可約多項式、特殊類型的多項式及多項式的某些性質四部分內容,詳細的介紹了多項式的基本內容及基本定理· 同時作者對於多項式的相關理論予以深刻...
高斯引理在代數(特別是環理論),如果一個整係數多項式的所有係數是互素的,則稱它是一個本原多項式,本原多項式對判定不可約多項式有很大幫助,高次多項式的不可約...
為有理係數多項式, 與 有公共根a,則 。定理3的意義是,若有理係數不可約多項式 有一根為另一有理係數多項式 的根,則 的全部根均為 的根。整...
每個次數不小於1的實係數多項式在實數域上都可以唯一地分解成一次因式與二次不可約因式的乘積。...
多項式的次數:多項式里,次數最高的項的次數,就是這個多項式的次數。齊次多項式:各項次數相同的多項式叫做齊次多項式。 不可約多項式:次數大於零的有理係數的多項式,不...
GF(q)中當q為素數冪時,那么GF(q)同構於GF(p)[x]/f(x),f(x)是GF(p)上的不可約n次多項式。例如在有限域GF(8)中,即GF(2`3),即在GF(2)上的3...
另一方面,如果F是代數閉域,那么根據前一個性質,以及對於任何域K,任何K[x]內的多項式都可以寫成不可約多項式的乘積,推出這個性質對F成立。...
圖埃定理(Thue theorem)有理逼近的一個重要定理.若n}3, f (z) =a"z"+a。一,z"-' + + a,z +a。是一個整係數的n次有理數域上的不可約多項式,則...
平凡因式亦稱當然因式,是多項式的一種特殊因式。若在數域P上給定多項式f(x),則P上任一個不等於零的常數以及與f(x)只相差一個非零常數因子的多項式都是f(x)...
初等代數一般在中學時講授,介紹代數的基本思想:研究當我們對數字作加法或乘法時會發生什麼,以及了解變數的概念和如何建立多項式並找出它們的根。代數的研究對象不僅是...
,它的極小多項式是奇次的。但是利用實數集的事實2,任何奇次數多項式在實數上有一個根,於是不存在奇次的且次數>1的不可約多項式。於是 是2的冪次。假設...
克羅內克定理(Kronecker theorem)關於代 數方程可根式解的命題.定理解釋設n為奇素數,f(二)是有 理數域上的n次不可約多項式,如果代數方程f.(二) 一0有根式解...
