定義
可分多項式在不同的作者的書下有兩個略微不同的定義。
最常見的一個定義是:當在一個給定域K上的多項式P(X)在K的代數閉包中有不同的根時,稱
多項式為可分的。換言之它的互異根的數量需要等於多項式的次數。在多項式因式分解的觀點下,這樣的多項式是無平方多項式。
第二個定義,當P(X)在K[X]中的每個不可約因子在K的代數閉包中的根互不相同,此時稱P(X)是可分的。這意味著每個不可約因子是無平方項的。在這個定義中,可分性依賴於K,比如任何一個不可分的不可約多項式P在它的分裂域上都變成可分的了。並且在這個定義下,每個域上的多項式是可分的,這包含了0特徵域和所有
有限域。
兩個定義對於K上不可約多項式是等價的,這個被用來定義域K的可分擴張。
在條目的餘下部分我們只用第一個定義。
一個多項式可分若且唯若它與它的形式導數P'(X)互素。
詳解
由於存在所謂的不可分不可約多項式或不可分元素——即這些元素是n次代數的,但它的共軛元素的個數小於n一伽羅瓦群的一般討論就變得複雜了.對某些特徵為p的域,這種複雜化就出現了,這可以用簡單的例子加以說明.
設K=Zp(u)表示模p整數的域Zp的單超越擴張,並設F表示由u^p=t生成的K的子域Zp(u^p).於是,F是由Zp上的超越元素t的所有有理形式組成.原來的元素u滿足F上的一個多項式方程f(x)=x^p—t=o.這個多項式f(x)在F=Zp(t)上實際上是不可約的,這是因為如果f在Zp(t)上可約,根據
高斯引理,在t的多項式整環Zp[t]上,f是可約的,但是,由於f(x)=x^p—t對於t來說是線性的,所以這樣的因式分解.f(x)=g(x,t)h(x,t)是不可能的.因此f(x)的根u在F上的次數是p.但是f(x)在K上有因式分解:f(x)=x^p一u^p=(x一u)^p.因此它只有一個根u,並且u(雖然它的次數p>1)除了它本身之外沒有其他共軛元素.
我們可以用下面的術語來描述上述情況.
定義 域F上的一個n次多項式f(x),如果它在某個根域N⊇F中有n個不同的根,那么稱它在域F上是可分的;否則,稱f(X)是不可分的.如果有限擴張K⊇F中每個元素在F上都滿足一個可分多項式方程,那么稱K在F上是可分的.
容易檢驗給定的多項式f(x)=a0+a1x+…+anXn是否是可分的.這也就是,首先根據公式f'(x)=a1+(2×a2)x+…+(n×an)x^(n-1)來定義f(x)的形式導數f'(x),這裡n×an表示an的n次自然倍數.如果這些係數都在實數域中,那么這種導數與微積分學中建立的普通導數是一致的.從形式導數的定義出發,不用任何極限概念,我們可以推導出很多微分法則,例如
(f+g)'=f'+g',(fg)'=fg'+f'g,(f^m)'=mf^(m-1)f',等等.
在任意根域N上把f(x)分解成不同線性因子的冪,
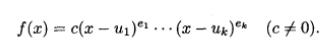 1
1把兩邊形式地微分,我們看到f'(x)是
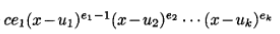 2
2與k一1項每項都包含(x-u1)^e1作為因子的和.因此當e1>1時,x—u1可整除f'(x),而當e1=1時,x一u1就不能整除f'(x).對e2,…,ek重複上述推理,我們得到f(x)和f'(x)有公因子,除非e1=e2=…=ek=1,即除非f(x)是可分的;因此f(x)在N上是可分的若且唯若f(x)和它的形式導數f'(x)是互素的.
相關定理
f(x)和f'(x)的最大公因式可用F[x]中的歐幾里得算法直接計算出來;當F擴張到較大的域上時,它們的最大公因式並不改變.於是我們得到
定理 設f(x)是域F上任意多項式,用歐幾里得算法計算f(x)和它的形式導數f'(x)的最大公因式d(x)(首一多項式).如果d(x)=1,那么,f(x)是可分的;否則f(x)是不可分的.
如果f(x)是不可約的,那么除非f(x)整除g(x),總有g.c.d.(f(x),g(x))=1,並且f(x)不能整除任意較低次的非零多項式.因此得到
推論1 任意不可約多項式是可分的,除非它的形式導數是零.
推論2 特徵為∞的域上的任意不可約多項式是可分的.
這是因為,當n>0,an≠0時,
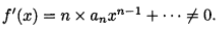 3
3進一步推論是:如果F的特徵是∞,那么任意n次不可約多項式f(x)的根域恰恰包含f(x)的n個不同的共軛根.而且,在特徵為∞的域上的任意代數數滿足一個不可約的因而也是可分的方程,所以特徵為∞的域的任意代數擴張,在上述意義之下是可分擴張.
推論2的結果對於素特徵的域是不成立的.例如,在不可約多項式f(x)=x^p—t有形式導數(x^p—t)'=p×x^(p-1)=0.
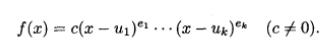 1
1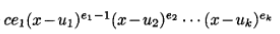 2
2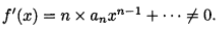 3
3
