可約多項式(reducible polynomial)一種特殊的多項式.指有非平凡因式的多項式。首先,多項式(polynomial)是指由變數、係數以及它們之間的加、減、乘、冪運算(非負整數次方)得到的表達式。可約多項式即這種表達是可以繼續簡化,沒有簡化到最簡形。
基本介紹
- 中文名:可約多項式
- 外文名:reducible polynomial
- 學科:數學
- 本質:代數式
定義
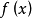
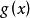
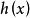
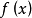
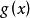
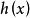
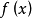
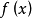
判定
定理1
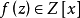
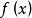
定理2
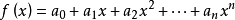
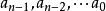
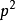
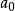
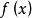
定理3
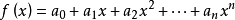
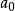
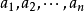
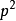
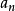
性質
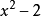

可約多項式(reducible polynomial)一種特殊的多項式.指有非平凡因式的多項式。首先,多項式(polynomial)是指由變數、係數以及它們之間的加、減、乘、冪運算(非負整數次方)得到的表達式。可約多項式即這種表達是可以繼續簡化,沒有簡化到最簡形。
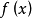
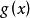
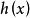
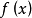
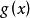
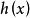
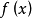
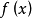
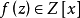
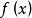
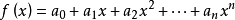
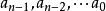
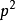
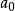
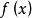
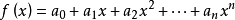
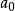
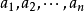
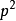
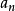
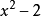
可約多項式(reducible polynomial)一種特殊的多項式.指有非平凡因式的多項式。首先,多項式(polynomial)是指由變數、係數以及它們之間的加、減、乘、冪運算(非負整數...
既約多項式又稱“不可約多項式”。次數大於零的有理數係數多項式,不能分解為兩個次數較低但都大於零的有理數係數多項式的乘積時,稱為有理數範圍內的“既約...
多項式中的每個單項式叫做多項式的項,這些單項式中的最高項次數,就是這個多項式的次數不可約多項式是一種重要的多項式,它在多項式環中有類似於素數在整數環中的地位...
一類重要的多項式.指既約因式在任意擴域內無重根的多項式.設f(x)是域F上次數大於零的多項式,若f(x)的每個既約因式在F的代數閉包內沒有重根,則稱f(x)為...
F[x]中任一個次數不小於 1的多項式都可以分解為F上的不可約多項式的乘積,而且除去因式的次序以及常數因子外,分解的方法是惟一的。 當F是複數域C時,根據代數基...
可約的概念滲透到數學的各個分支, 它在不同的分支中有不同的表現形式。與可約概念相對的就是不可約。...
有理係數多項式是高等代數裡面多項式因式分解討論的一個特例。我們知道,每個次數大於等於1的有理係數多項式都能惟一地分解成不可約的有理係數多項式的乘積。但是對於...
本書分為多項式的根、不可約多項式、特殊類型的多項式及多項式的某些性質四部分內容,詳細的介紹了多項式的基本內容及基本定理· 同時作者對於多項式的相關理論予以深刻...
每個次數不小於1的實係數多項式在實數域上都可以唯一地分解成一次因式與二次不可約因式的乘積。...
多項式分裂域(splitting field of a polynomial )與多項式相關的一種域。 在抽象代數中,具有域中係數的多項式分裂域是該域的最小域延伸,多項式在該域上分裂為線性...
GF(q)中當q為素數冪時,那么GF(q)同構於GF(p)[x]/f(x),f(x)是GF(p)上的不可約n次多項式。例如在有限域GF(8)中,即GF(2`3),即在GF(2)上的3...
設p(x) 為不可約多項式. 如果f(x)能被p(x) 的k次方整除而p(x)的k+1次方不能, 則稱p(x) 是 f(x)的k 重因式...
2 高等代數定義 3 不可約多項式 平凡因式簡介 編輯 平凡因式亦稱當然因式,是多項式的一種特殊因式。若在數域P上給定多項式f(x),則P上任一個不等於零的常數以...
多項式的次數:多項式里,次數最高的項的次數,就是這個多項式的次數。齊次多項式:各項次數相同的多項式叫做齊次多項式。 不可約多項式:次數大於零的有理係數的多項式,不...
分解後二分式的分母均為不可約多項式,分子次數比分母低,符合上述的條件。簡單來說,部分分式分解的目的是將以下型式的有理函式:其中f和g均為多項式,轉換為以下的...
2.5.1 多項式的根2.5.2 多項式函式2.5.3 複數域上的不可約多項式§2.6 實數域上的不可約多項式§2.7 有理數域上的不可約多項式...
