基本介紹
定義
與質元素的關係
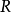
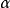

套用




舉例



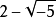

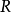
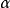








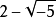
不可約元素是抽象代數中的名詞,是指在整環或者非整環中一個非零、非單位的元素,而且也無法表示為二個非單位元素的乘積。結一不可約元素和交一不可約元素統稱...
本原元素定理簡介 編輯 在數學中,本原元素定理精確刻畫了什麼時候對於一個域擴張E/F,E可以表示為F(α)的形式,即E可以由單個元素生成。...
在數學裡,尤其是在抽象代數裡,交換環的素元(prime element)是指滿足類似整數里的素數或不可約多項式之性質的一個數學物件。須注意的是,素元與不可約元素之間並...
“一次多項式是不可約的”的斷言對於任何域都是正確的。如果F是代數閉域, 是...與若干個形為a/(x−b)n的有理函式之和,其中n是自然數,a和b是F的元素...
如果F是代數閉域,p(x)是F[x]的一個不可約多項式,那么它有某個根a,因此p...個形為a/(x − b)^n的有理函式之和,其中n是自然數,a和b是F的元素。...
既約因式在F的代數閉包內沒有重根,則稱f(x)為可分多項式;否則,稱為不可分...於是,F是由Zp上的超越元素t的所有有理形式組成.原來的元素u滿足F上的一個...
5-1.對稱圖象的對稱元素系5-2.有限圖象和點陣圖象5-3.第一類和第二類對稱群...第三章 有限點群的不可約表象§8.不可約表象的正交組元系定理...
單項表示(monomial representation)一類特殊的線性表示.一個n階方陣,若它的每行及每列至多只有一個元素不為零,則稱這個方陣為單項矩陣.設ρ是群G的一個線性表示...
對於一個數域P,如果ξ是域P上的一個不可約多項式在其擴域上的一個根,我們把ξ和域P的元素之間的和、差、積、商所組成的數集叫做域P上的一個代數擴張。...
5-1.對稱圖象的對稱元素系 5-2.有限圖象和點陣圖象 5-3.第一類和第二類對稱...第三章 有限點群的不可約表象 §8.不可約表象的正交組元系定理 8-1.正交...
