基本介紹
- 中文名:異面直線所成角
- 概念:過空間任意一點引兩條直線分別平行於兩條異面直線,它們所成的銳角(或直角)就是異面直線所成的角
- 範圍:θ∈(0°,90°]
- 所屬學科:數學
分類
異面直線
公垂線
兩條直線垂直
求法
幾何法
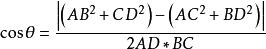
向量法
- 向量幾何法。運用向量的加減法規則,把要求的異面直線用向量表示,並運用向量的運算法則(例如分配律、共線向量)來求出cosθ
- 向量代數法。當容易找到三條兩兩垂直的直線時,可以以它們的交點為坐標軸原點建立直角坐標系,運用代數方法計算。

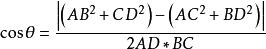
過空間任意一點引兩條直線分別平行於兩條異面直線,它們所成的銳角(或直角)就是異面直線所成的角。角的範圍是θ∈(0°,90°](注:當所成角為90°時,兩...
異面直線所成的角是指分別平行於兩條異面直線的兩相交直線所成的角。...... 異面直線所成的角是指分別平行於兩條異面直線的兩相交直線所成的角。...
異面直線是不在同一平面上的兩條直線。異面直線是既不相交,又不平行的直線。因為兩條直線如果相交或平行,則它們必在同一平面上。若無特別的說明,所說的空間...
來求異面直線所成角θ。利用該方法求θ必須先由圖像判斷二面角是銳角還是鈍角。如果是銳角,那么取正號;鈍角,那么取負號。待求出θ以後,如果二面角是銳角,那么二面角...
7.異面直線的距離法:設二面角為C-AB-D,其中AC和BD互為異面直線且AC⊥AB,BD⊥AB(即AB是異面直線AC和BD的公垂線)。利用該方法求異面直線所成角θ,必須先...
空間的兩條直線有以下三種位置關係:1.相交直線,2.平行直線,3.異面直線。...... a、b'∥b.我們把 直線a'和b'所成的銳角(或直角)做異面直線a和b所成的角...
空間角度(Space angle),把立體幾何學的異面直線所成的角、直線與平面所成的角、平面與平面所成的角,統稱為空間角度。...
(5)三垂線定理的實質是平面的一條斜線和平面內的一條直線垂直的判定定理。(6)可用來解決異面直線所成的角和二面角的平面角等問題。...
而一旦l不經過點A,則l和OA互為異面直線(平面的一條斜線和平面內不經過斜足的直線互為異面直線),根據異面直線所成角的定義,l和OA所成角即為∠OAC。也就是...
這個理論體系中的主要內容是:點、直線、平面的位置關係;各種空間角(異面直線所成的角、直線與平面的夾角、二面角、多面角等)的性質;各種簡單幾何體(多面體、旋轉體...
§2.空間兩條直線 (1)空間兩條直線的位置(48一54) (2)空間多邊形(55―74) (3)異面直線所成的角(75―85) (4)異面直線間的距離(86―98) (5)異面直...
三、空間向量與空間角的關係核心考點解讀考點一空間向量及其線性運算考點二利用空間向量證明平行、垂直關係考點三利用空間向量求異面直線所成的角、線面角...
158.如何求兩條異面直線所成的角? 159.如何求兩條異面直線的距離? 160.已知直線α、b, 過空間一點A與直線α和 直線b都成60°角的直線有幾條? 161.是否...
什麼是異面直線所成的角? 什麼是二面角?什麼是二面角的平面角? 1.2角概念和角大小的上位數學知識對教學的啟示 1.2.1角概念的上位數學知識對教學的啟示 ...
2.空間兩條直線 (1)空間兩條直線的位置(13―14) (2)空間多邊形(15-21) (3)異面直線所成的角(22-26) (4)異面直線間的距離(27-40) 3.空間直線和平面...
5.5直線、平面垂直的判定與性質 題源1直線與平面垂直 題源2平面與平面垂直 題源3直線與直線垂直 5.6空間中的角和距離 題源1異面直線所成的角 題源...
模型3異面直線所成角214模型4直線與平面所成角216模型5二面角217模型6與摺疊有關的問題218題型7圓錐曲線綜合解答題的解題模板模型1直線與圓錐曲線位置關係問題219...
易錯點4異面直線所成角理解錯誤 易錯點5空間點、線、面位置關係判斷錯誤 易錯點6線面位置關係定理使用不當 第三章直線與方程 易錯點1直線傾斜角與斜率關係...
88.異面直線的距離89.直線和平面垂直的性質90.平面的法向量91.點到平面的距離92.直線和平面所成的角93.向量在平面內的射影94.平面與平面平行的性質...
54 《同角公式之錯解舉例》 2004.2 考試報(高一版) 55 《平移法求異面直線所成的角》 2004.2 數學學習指導(高二版) 56 《例析圓錐曲線中的對稱問題》...
121 用向量法研究空間直線與平面的位置關係 122 用向量法研究空間平面與平面的位置關係 123 異面直線所成角公式 124 直線與平面所成角公式 125 二面角公式...
兩條異面直線所成的角 兩條異面直線互相垂直 兩條異面直線的公垂線 兩條異面直線的距離 直線與平面平行的定義 直線與平面的位置關係 直線與平面平行的...
6.2空間直線 6.2.1空間兩條直線的位置關係 6.2.2空間的平行直線 6.2.3異面直線所成的角 6.3直線與平面的位置關係 6.3.1直線與平面的位置關係分類...
6求異面直線所成的角 7平移過程中的空間想像能力 能力測試點39 直線、平面平行的判定與性質 1直線與平面平行 2平面與平面平行 3線面平行的證明 4面...
第42例 異面直線 第43例 異面直線所成的角 第44例 三垂線定理 第45例 直線和平面所成的角 第46例 二面角(1) 第47例 二面角(2) 第48例 異面直線的距離...
