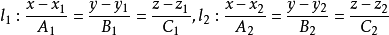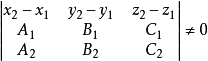異面直線是不在同一平面上的兩條直線。異面直線是既不相交，又不平行的直線。因為兩條直線如果相交或平行，則它們必在同一平面上。若無特別的說明，所說的空間直線，都是指異面直線。
基本介紹
- 中文名：異面直線
- 外文名：skew lines
- 定義：不同在任何一個平面內的兩條直線
- 判定定理：不經過交點的直線
- 特點：既不平行，也不相交
- 學科：數學
定義,相關概念,判定方法,性質,
定義
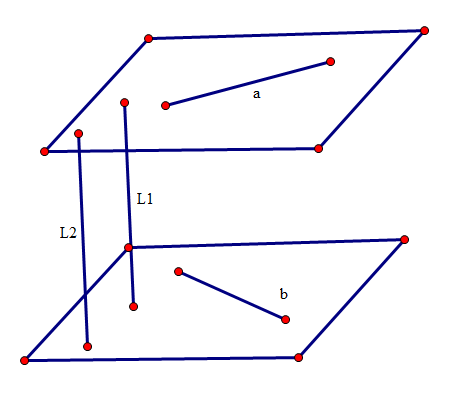
不同在任何一個平面內的兩條直線叫做異面直線。空間兩條直線的位置關係有三種，即相交和平行，這兩種情況的兩條直線在同一平面內。另外一種情況就是不相交也不平行稱為異面直線。
注意，以下關於異面直線的說法是錯誤的：
1．分別在兩個平面內的直線是異面直線；
2．在空間不相交的兩條直線是異面直線；
3．平面內的一條直線和平面外的一條直線是異面直線。
相關概念
1.兩條異面直線所成的角
直線a、b是異面直線。經過空間任意一點o，分別引直線a'//a，b'//b。直線a'和b'所成的銳角(或直角)叫做異面直線a和b所成的角。兩條異面直線a、b所成角的大小，只由a、b的相互位置來確定，與點o的選擇無關(可以用等角定理來證明)。
2.兩條異面直線的距離
兩條異面直線的公垂線茫這兩條異面直線問的線段的長度，叫做兩條異面直線的距離。
異面直線a、b間的距離，也就是a和過b且平行於a的平面M間的距離。
判定方法
(1)定義法：由定義判定兩直線永遠不可能在同一平面內，常用反證法。
(2)判定定理：過平面外一點與平面內一點的直線和平面內不經過該點的直線是異面直線。
例證：
判定定理：平面的一條交線與平面內不經過交點的直線互為異面直線。
已知：AB∩α=A，CD⊂α，A∉CD。求證：AB和CD互為異面直線。
證明：假設AB和CD在同一平面內，設這個平面是β。即A∈β，CD⊂β。
∵A∈α，CD⊂α，A∉CD
由不在同一直線上的三個點確定一個平面可知，α和β重合。
∵AB⊂β
∴AB⊂α，這與已知條件AB∩α=A矛盾。
∴AB和CD不在同一平面內，即AB和CD互為異面直線
（3）解析幾何
設兩條空間直線
則它們互為異面直線的充要條件是行列式
性質
- 和兩條異面直線都垂直相交的直線叫做兩條異面直線的公垂線。
- 兩條異面直線的公垂線在這兩條異面直線間的線段，叫做這兩條異面直線的公垂線段，公垂線段的長度，叫做兩條異面直線的距離。
- 過平面外一點與平面內一點的直線，和平面內不經過該點的直線是異面直線。
- 經過兩條異面直線中的一條，有一個平面與另一條直線平行。
- 異而冉直線的公垂線存在且唯一。
- 在兩條異面直線上各任取一點，這兩點形成的所有線段中這兩條異面直線的距離最小。
