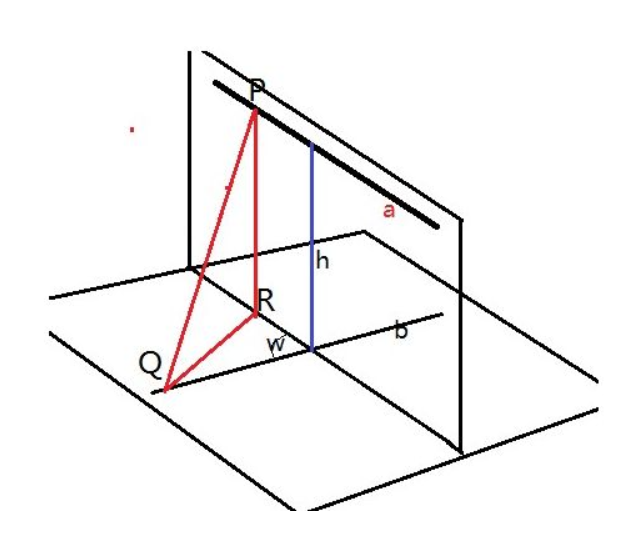
一條直線同時垂直於兩條或兩條以上線段或直線,這條直線就是被垂直的線段或直線的公垂線。然而,如同兩條異面直線的公垂線夾在異面直線間的部分,這才被叫做公垂線段。
基本介紹
- 中文名:公垂線
- 外文名:Male vertical line
- 所屬學科:幾何
- 套用:數學
- 定義:一條直線同時垂直與兩條以上直線
概念,引申含義,異面直線的公垂線,定義,定理,基於公垂線約束的立體視覺建模方法,基於公垂線約束的立體視覺建模,實驗數據分析,研究結論,
概念
例如線段a垂直於線段b,同時也垂直於線c,甚至更多的d、e、f……那么線段a就是線b、c的或者是d、e、f的公垂線。
引申含義
兩條直線不在公垂線上經過同一點,這兩條直線必不交叉。 圖例
圖例
 圖例
圖例兩條直線經過公垂線上的同一點,這兩條直線所在的平面,必定垂直於公垂線,並且這個平面必垂直於他們和公垂線組成的平面。
公垂線可以和被垂直的線段或者直線在一個平面內,也可以不在一個平面內。公垂線可以和被垂直對象交叉,也可以不交叉。
如圖所示,AB都是CD和EF的公垂線。
異面直線的公垂線
定義
同時和兩條異面直線垂直相交的直線,叫做異面直線的公垂線。兩個交點之間的線段長度,叫做異面直線的距離。
定理
任意兩條異面直線有且只有一條公垂線,證明:
(1)存在性
設m、n是兩條異面直線,過m上一點P作直線a∥n,則m和a確定一個平面α。
過P作直線b⊥α,則b⊥m,b⊥a,b⊥n,且b和m確定一個平面β。
∵m、n異面
∴n不在β內
且n不會與β平行,這是因為如果n∥β,則a∥β或a⊂β
∵P∈β,P∈a
∴a與β不平行
若a⊂β,∵b⊥m,b⊥a,m∩a=P
∴a和m重合,即m∥n,矛盾
∴n與β不平行,即n和β相交
設這個交點為Q,即Q∈β,過Q作直線l⊥m,則l∥b
∴l⊥n,即l同時垂直m、n,且l和m、n交點分別為P、Q
(2)唯一性
由存在性的證明可知n和β只有一個交點Q,經過Q點有且只有一條直線l⊥m,因此異面直線的公垂線有且只有一條。
基於公垂線約束的立體視覺建模方法
基於人類視覺系統理論的雙目立體視覺,運用兩台相機對同一景物從不同位置成像,獲得景物的立體圖像對,通過各種算法匹配出相應像點,從而利用視差恢復深度信息。由於具有成本低、解析度高、無破壞和數據獲取速度快等優點,立體視覺被公認為最有前途的三維坐標測量方法。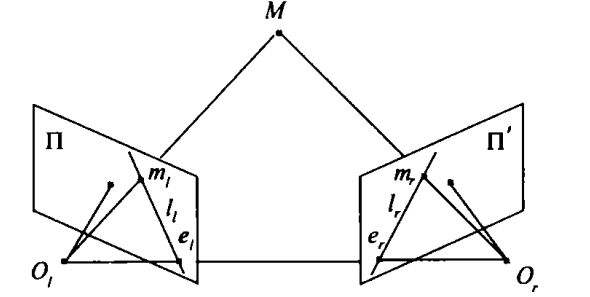 圖1 立體視覺理想成像模型
圖1 立體視覺理想成像模型
 圖1 立體視覺理想成像模型
圖1 立體視覺理想成像模型立體視覺測量根據視差原理完成空間三維點坐標測量,是典型的空間交會問題。理想情況下,如圖1所示,通過光學中心點Ot和Or的兩相機所成的圖像點mt和mr,其反投射線應當相交於一點(空間特徵點)M。這5點都位於2條相交線OtM和OrM形成的外極平面上。特別地,點mr位於該平面與第二台相機的視平面的交線lr上。直線lr是與點mr相關的外極線,它經過點er。er是連線兩個光學中心Ot和Or的基線和平面的交點。同樣,點mt位於點mt關聯的直線ll上,且該直線經過基線和平面的交點et。但是由於相機的內參數、圖像點的定位以及兩相機之間的相互空間姿態的確定等各種誤差的存在,射線Olml和Ormr不能在三維空間中精確相交或嚴格交於一點,因此,立體視覺測量中空間點坐標的求解問題就變成了最小化問題。
為了獲得兩相機參數已知的三維重建空間點坐標的最優解,常用的方法主要有:1)線性三角建模方法,該方法是與DLT方法相似的一種常用的方法,算法簡單,而且計算速度快,但它是一種純代數的重建三維空間點算法,沒有任何幾何意義;2)中點法,該方法直接選取兩條反投射線的公垂線段中點作為空間點坐標,它雖然使得空間點到兩條反投射線的距離的平方和最短,但它並未考慮其它因素的影響,Hartley和Beardsley均證明該方法的重建精度在多數情況下不如線性三角法精度高;3)基於對極約束的建模方法,它以滿足對極約束為條件,求兩像點附近與實際像點的距離平方和最短的點作為兩像點的估計值,然後再由其它任何三角法求得空間點。該方法能很好地克服噪聲的影響,但它運算時間長,效率低,由於它只考慮了圖像點的誤差,沒有考慮空間的距離誤差,所以在歐氏重建中,它的重建精度低於上述兩種方法。
在綜合考慮空間距離誤差以及圖像點誤差的基礎上,提出了基於公垂線約束的立體視覺建模方法,該方法不僅保證了所求空間點到兩條反投射線之間的距離最短,而且還消除了圖像點誤差以及空間點距兩相機位置不同而造成的影響,使得所求的空間點在兩像平面上的投影誤差最小。
基於公垂線約束的立體視覺建模
該建模方法首先以空間點到兩條反投射線的距離最小為目標函式,確定公垂線約束;然後通過最小化空間點在兩像平面上的投影誤差求得空間點的最優解。
(1)公垂線約束的確定
為了最小化重建空間點的空間距離誤差,必須使得空間點坐標到兩圖像點對應的反投射線的距離最短。根據異面直線的距離定理:兩條異面直線的公垂線段是分別連結兩條異面直線上兩點的線段中最短的一條,因此所求空間點必須在兩條反投影射線的公垂線段上,如圖2所示。 圖2 基於公垂線 約束的立體 視覺 建模方法
圖2 基於公垂線 約束的立體 視覺 建模方法
 圖2 基於公垂線 約束的立體 視覺 建模方法
圖2 基於公垂線 約束的立體 視覺 建模方法(2)空間點的最優估計
兩條反投射線的公垂線段上的所有點均滿足到兩條反投射線的距離最短的條件,但由於空間點距兩相機位置的不同,公垂線上不同的空間點在兩像平面的投影與實際像點的誤差不同,為了減小圖像點誤差以及空間點距兩相機位置不同而造成的影響,本文提出了基於公垂線約束的投影誤差最小化建模方法,該方法的以空間點在射線Olml和Ormr的公垂線段上為約束,以圖像點觀測值與估計值之間的誤差作為最小化目標函式獲得空間點的最優解。
實驗數據分析
綜合仿真以及實際數據的對比實驗,由表1和表2,可以得出如下結論:1)4種方法的三維重建誤差均隨著圖像噪聲水平的增加而變大,所以在立體視覺測量系統中,應該儘量減小圖像誤差的影響;2)基於外極線約束法的重構誤差最大,因為該方法的最小化目標是圖像點測量值與實際值之間的誤差,沒有考慮空間距離誤差的影響,所以該方法得到的空間點坐標誤差相對來講較大;3)中點法是以空間點坐標到對應射線的距離平方和作為目標函式,雖然它保證了空間點到兩條反投射線的距離平方和最小,但是由於它沒有考慮圖像點誤差對空間點重構精度的影響,所以中點法的重建精度比線性三解法的低;4)基於公垂線約束法由於同時考慮空間距離誤差以及圖像點噪聲誤差的影響,所以無論是在仿真數據中,還是實際量塊的測量中,它的三維重建精度都要高於其它三種常用的重建算法,並且在圖像誤差為0.04個像素的範圍內,基於該重建算法的立體視覺測量系統的測量精度能達到0.023mm。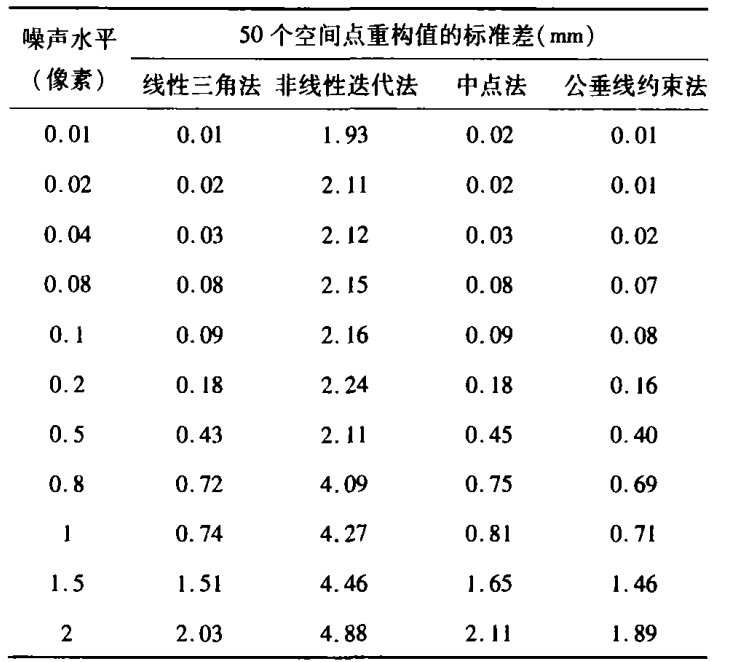 表 1 不同噪聲水平下四種方法的50個空間點的重構標準差
表 1 不同噪聲水平下四種方法的50個空間點的重構標準差
 表 1 不同噪聲水平下四種方法的50個空間點的重構標準差
表 1 不同噪聲水平下四種方法的50個空間點的重構標準差研究結論
從實驗結果來看,研發方法的三維重建誤差要低於其它幾種重建算法。同時由於採用公垂線段中點作為以空間點在兩像平面上的投影誤差為最小化目標函式的非線性疊代的初始值,所以該方法能夠快速、有效地收斂到空間點的最優解。因此,研究方法在綜合考慮空間距離誤差以及圖像點誤差的基礎上,提高了空間點的重建精度。 表2 測量長度誤差結果
表2 測量長度誤差結果
 表2 測量長度誤差結果
表2 測量長度誤差結果