在數學中,曲線積分是積分的一種。積分函式的取值沿的不是區間,而是特定的曲線,稱為積分路徑。曲線積分有很多種類,當積分路徑為閉合曲線時,稱為環路積分或圍道積分。曲線積分可分為:第一類曲線積分和第二類曲線積分。
基本介紹
- 中文名:曲線積分
- 外文名:Line Integral
- 基本簡介:∫ρ(x,y)ds叫對弧長的曲線積分
- 定義:弧長曲線積分也叫第一類曲線積分
- 類別:第一、二類曲線積分
- 套用:重力場或電場等
引例

定義
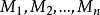
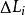

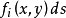


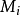





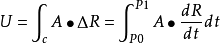
分類
相關概念
積分聯繫


在數學中,曲線積分是積分的一種。積分函式的取值沿的不是區間,而是特定的曲線,稱為積分路徑。曲線積分有很多種類,當積分路徑為閉合曲線時,稱為環路積分或圍道積分。曲線積分可分為:第一類曲線積分和第二類曲線積分。

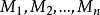
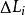

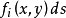


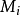





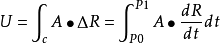

在數學中,曲線積分是積分的一種。積分函式的取值沿的不是區間,而是特定的曲線,稱為積分路徑。曲線積分有很多種類,當積分路徑為閉合曲線時,稱為環路積分或圍道積分...
定義在平面曲線或空間曲線上的函式關於該曲線的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲線,計算該曲線的質量。...
第二型曲線積分亦稱關於坐標的曲線積分,是一種與曲線定向有關的曲線積分,與第一型曲線積分相比,從物理意義上,可以看出兩種曲線積分是不同的,儘管它們都是沿著曲線...
對於滿足一些條件的曲線,起點和終點的位置固定,沿不同的路線積分,其積分值相同,即曲線積分只與起點和終點有關,與路線的選取無關。...
定義在曲面上的函式關於該曲面的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲面,計算該曲面的質量。...
高斯積分是在機率論和連續傅立葉變換等的統一化等計算中有廣泛的套用。在誤差函式的定義中它也出現。雖然誤差函式沒有初等函式,但是高斯積分可以通過微積分學的手段...
第二型曲面積分是關於在坐標面投影的曲面積分,其物理背景是流量的計算問題。第二型曲線積分與積分路徑有關,第二型曲面積分同樣依賴於曲面的取向,第二型曲面積分與...
積分輪換對稱性是指坐標的輪換對稱性,簡單的說就是將坐標軸重新命名,如果積分區間的函式表達不變,則被積函式中的x,y,z也同樣作變化後,積分值保持不變。...
積分檢驗法是汽液平衡數據熱力學一致性檢驗的一種較常用的方法,由於實驗測定汽液平衡數據時往往控制在等溫或等壓條件下,故汽液平衡數據的一致性檢驗也分為等溫和...
積分變換無論在數學理論或其套用中都是一種非常有用的工具。最重要的積分變換有傅立葉變換、拉普拉斯變換。由於不同套用的需要,還有其他一些積分變換,其中套用較為...
《高等數學第Ⅲ卷多元微積分與微分幾何初步》是1997年清華大學出版社出版的圖書,作者是蕭樹鐵。...
解析曲線(analytic curve)是複平面上的基本概念之一。複數平面即是z=a+bi,它對應的坐標為(a,b)。其中,a表示的是複平面內的橫坐標,b表示的是複平面內的縱...
積分學(integral calculus)數學分析的分支學科。即研究各種積分(理論、計算和套用)以及它們之間的關係的學科。積分學也是高等數學的基礎學科之一。積分學的研究對象...
《數學題解辭典(初等微積分)》是上海辭書出版社出版的圖書。...... 第八章 重積分、曲線積分和曲面積分 1. 重積分 (1)二重積分(1317―1333) (2)三重積分和...
超橢圓積分其積分值完全由L本身的起始點和終點所確定,和Abel積分的一般情形一樣,任何超橢圓積分均可表示成一些初等函式和具有特殊形式的第一、二、 三類典範超橢圓...
柯西積分定理(或稱柯西-古薩定理),是一個關於複平面上全純函式的路徑積分的重要定理。柯西積分定理說明,如果從一點到另一點有兩個不同的路徑,而函式在兩個路徑...
環量(circulation)是流體的速度沿著一條閉曲線的路徑積分,通常用Γ來表示。一個矢量沿一條封閉曲線積分,得到的結果叫環量。環量控制由邊界層控制發展而來,目前已...
格林公式是一個數學公式,它描述了平面上沿閉曲線L對坐標的曲線積分與曲線L所圍成閉區域D上的二重積分之間的密切關係。一般用於二元函式的全微分求積。...
斯托克斯公式是微積分基本公式在曲面積分情形下的推廣,它也是格林公式的推廣,這一公式給出了在曲面塊上的第二類曲面積分與其邊界曲線上的第二類曲線積分之間的聯繫。...
斯托克斯公式是格林公式的另一推廣,是把具有光滑或分段光滑的邊界曲線的光滑曲面上的曲面積分與其邊界上的曲線積分聯繫起來。...
斯托克斯定理(英文:Stokes' theorem)是微分幾何中關於微分形式的積分的一個命題,它一般化了向量微積分的幾個定理,以斯托克斯爵士命名。當封閉周線內有渦束時,則沿...
