解析曲線(analytic curve)是複平面上的基本概念之一。複數平面即是z=a+bi,它對應的坐標為(a,b)。其中,a表示的是複平面內的橫坐標,b表示的是複平面內的縱坐標,表示實數a的點都在x軸上,所以x軸又稱為“實軸”;表示純虛數b的點都在y軸上,所以y軸又稱為“虛軸”。
基本介紹
- 中文名:解析曲線
- 外文名:analytic curve
- 領域:數學
- 學科:複數
- 方程:參數方程
- 對象:冪級數
概念

複平面
參數方程

冪級數



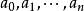

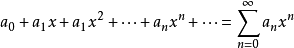

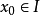
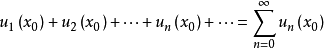


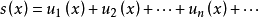

解析曲線(analytic curve)是複平面上的基本概念之一。複數平面即是z=a+bi,它對應的坐標為(a,b)。其中,a表示的是複平面內的橫坐標,b表示的是複平面內的縱坐標,表示實數a的點都在x軸上,所以x軸又稱為“實軸”;表示純虛數b的點都在y軸上,所以y軸又稱為“虛軸”。





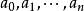

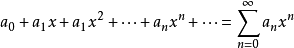

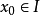
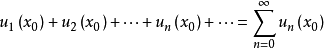


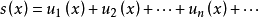

解析曲線(analytic curve)是複平面上的基本概念之一。複數平面即是z=a+bi,它對應的坐標為(a,b)。其中,a表示的是複平面內的橫坐標,b表示的是複平面內的縱...
維維亞尼曲線(Viviani curve)是一種特殊曲線,球面x²+y²+z²=a²與圓柱面x²+y²-ax=0的交線。它的參數方程可寫作r(t)=(a cos²θ,a cos...
實際工作中,變數間未必都有線性關係,如服藥後血藥濃度與時間的關係;疾病療效與療程長短的關係;毒物劑量與致死率的關係等常呈曲線關係。曲線擬合(curve fitting)是...
曲線,是微分幾何學研究的主要對象之一。直觀上,曲線可看成空間質點運動的軌跡。微分幾何就是利用微積分來研究幾何的學科。為了能夠套用微積分的知識,我們不能考慮...
完全解析函式(complete analytic function) 亦稱整體解析函式,一類大範圍解析函式中一個解析元素的全部解析開拓所確定的函式稱為由這個解析元素生成的完全解析函式,它的...
《收益率曲線解析》是2009年企業管理出版社出版的圖書,作者是喬德里。...... 《收益率曲線解析》是由喬德里(英國)編寫,企業管理出版社出版的一本金融經濟學教科...
在工程設計或科學實驗中所得到的數據往往是一張關於離散數據點的表 ,沒有解析式來描述 x-y關係。根據所給定的這些離散數據點繪製的曲線,稱為不規則曲線,通常用...
具有某種共同性質的所有曲線的集合,稱為一個曲線系,並用含有一個參數的方程來表示。... 涉及 解析幾何 特徵 曲線系方程的特徵 :對於x,y的二元方程,如果在方程中...
曲線相關(curve correlation)亦稱“非線性相關”。在兩個變數單相關場合,其散點圖散布於某條曲線附近,進行回歸分析時宜用非線性回歸模型代表其間的相關關係。測度...
空間曲線(space curves)是經典微分幾何的主要研究對象之一,在直觀上曲線可看成空間一個自由度的質點運動的軌跡。研究空間曲線的有力工具是微積分,我們可以用微積分...
常態分配曲線反映了隨機變數的分布規律。理論上的常態分配曲線是一條中間高,兩端逐漸下降且完全對稱的鐘形曲線。...
重要科技業者宏碁集團創辦人施振榮先生,在1992年為“再造宏碁”提出了有名的“微笑曲線”(Smiling Curve)理論,以作為宏碁的策略方向。經歷了十年多以迄今日,施振榮...
連續曲線(continuous curve)是複平面上的拓撲基本概念之一,閉線段a≤t≤b(a≠b)到複平面的連續映射稱為連續曲線。若x(t)和y(t)是兩個在區間a≤t≤b上...
垂足曲線(pedal curve)是一種平面曲線,即由一已知曲線所產生的另一曲線。給定一條曲線C和一個定點O,從點O向曲線C的任一條切線作垂線,垂足M的軌跡S稱為曲線C...
解析函式分支(branch of analytic function ) 由完全照一析函式的一個函式元素在區域內的解析開拓所得的函式元素之全體.設f(z)是一個完全解析函式,P(z;a)是f...
金屬材料的蠕變過程常用變形與時間之間的關係曲線來描述,這樣的曲線稱為蠕變曲線。室溫拉伸試驗時,長期保持屈服極限以下的應力,試件不會產生塑性變形,也就是說應力-...
S型生長曲線,指的是當種群在有限資源里生長,其生長符合邏輯斯諦微分方程,隨時間變化的生長曲線就呈S形狀。在數學上,它是邏輯斯諦微分方程的解析解。...
曲線幻覺是指豎線似乎是彎曲的,但其實他們是筆直而相互平行的。當你的視網膜把邊緣和輪廓譯成密碼,幻覺就偶然地現在視覺系統發生。事實上壓力越大的人越容易認為是...
數學中有各式各樣富含詩意的曲線,螺旋線就是其中比較特別的一類。螺旋線這個名詞來源於希臘文,它的原意是“旋卷”或“纏卷”。例如,平面螺旋便是以一個固定點...
