基本介紹
- 中文名:希爾伯特轉換
- 外文名:Hilbert transform
- 領域:數學與信號處理
- 命名人物:大衛·希爾伯特
概述
歷史
定義
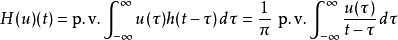
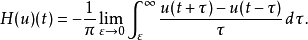
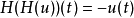
特性
邊界
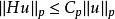
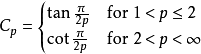
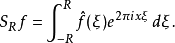
反自伴性
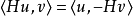
逆變換
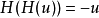
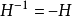
微分
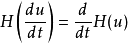
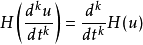
卷積
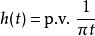
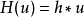
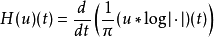
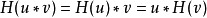
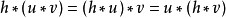
不變性
- 可與運算元Taƒ(x)=ƒ(x+a)交換,對所有實數a
- 可與運算元Mλƒ(x)=ƒ(λx)交換,對所有λ>0
- 可與鏡射Rƒ(x)=ƒ(−x)反交換
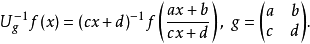
頻率回響
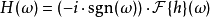

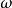
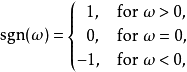
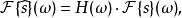
反(逆)希爾伯特變換
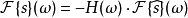
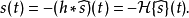

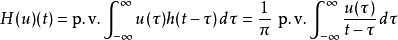
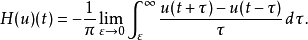
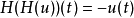
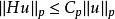
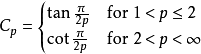
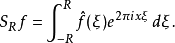
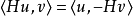
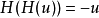
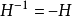
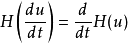
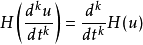
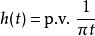
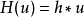
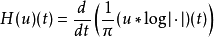
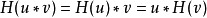
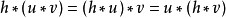
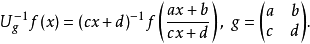
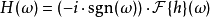

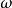
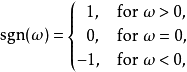
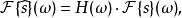
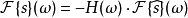
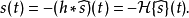
在數學與信號處理的領域中,一個實值函式的希爾伯特變換(Hilbert transform)——在此標示為H——是將信號s(t)與1/(πt)做卷積,以得到s'(t)。因此,希爾伯特...
在數學和信號處理中,希爾伯特變換(Hilbert transform)是一個對函式產生定義域相同的函式的線性運算元。...
希爾伯特-黃轉換(Hilbert-Huang Transform),由台灣中央研究院院士黃鍔(Norden E. Huang)等人提出,將欲分析數據分解為本質模態函式(intrinsic mode functions, IMF),...
了經驗模態分解方法,並引入了Hilbert譜的概念和Hilbert譜分析的方法,美國國家航空和宇航局(NASA)將這一方法命名為Hilbert-Huang Transform,簡稱HHT,即希爾伯特-黃變換...
里斯變換是一種積分變換,屬於微積分學科。當n=1時,里斯變換恰恰就是熟知的希爾伯特變換,可見里斯變換的概念是希爾伯特變換的推廣。...
在數學調和分析中,里茲變換是一族對於空間維數大於1的希爾伯特變換的推廣。...... 在數學調和分析中,里茲變換是一族對於空間維數大於1的希爾伯特變換的推廣。...
么正變換定義1 么正算符是希爾伯特空間H上的有界線性運算符U:H→H,滿足U*U =UU*=I,其中U*是U的伴隨矩陣,I:H→H是個體算符。...
關於數學變換,既涉及傅立葉變換、Z變換、拉普拉斯變換、小波變換、希爾伯特變換、沃爾什變換、數論變換等正交變換,也涉及一類特殊的非線性變換:同態變換.關於估計方法,...
傅立葉變換的線性,是指兩函式的線性組合的傅立葉變換,等於這兩個函式分別做傅...(DSP),有許多的變換:傅立葉變換、拉普拉斯變換、Z變換、希爾伯特變換、離散餘弦...
凱萊變換在對稱運算元和部分等距離運算元之間建立了一種對應關係。設𝓗是希爾伯特空間, 是閉對稱運算元,則 都是單射,且其指域 都是𝓗的閉子空間。定義了從 到 上...
其中虛數項為實數訊號的希爾伯特轉換(Hilbert Transform),將它定義為。稱作解析函式的理由是,此型式的複數函式滿足柯西-里曼(Cauchy-Riemann)的可微分條件,稱之為解析...
在數學和信號處理中,解析信號(英語:analytic signal)是沒有負頻率分量的復值函式。 解析信號的實部和虛部是由希爾伯特變換相關聯的實值函式。...
3.7.3利用傅立葉變換性質和常見信號的傅立葉變換對3.8LTI系統的頻域分析3.8.1頻率回響3.8.2信號無失真傳輸3.8.3理想低通濾波器的回響3.9希爾伯特變換...
5.6 利用希爾伯特變換研究系統函式的約束特性5.7 調製與解調5.8 帶通濾波系統的運用5.9 從抽樣信號恢復連續時間信號5.10 脈衝編碼調製(PcM)...
離散變換和快速算法、數字頻譜分析、數字濾波器設計和實現、希爾伯特變換和復倒譜、多採樣率處理等,構成了離散信號處理的基本知識體系; 第9~12章介紹了幾個與實際...
全書共9章,包括:緒論;連續時間系統的時域分析;傅立葉變換;拉普拉斯變換、連續...5.6 利用希爾伯特變換研究系統函式的約束特性5.7 調製與解調5.8 帶通濾波系統的...
7.4.3 FIR希爾伯特變換器和FIR數字微分器設計 (209)7.5 FIRDF與IIRDF的比較 (213)習題與上機題 (214)第8章 時域離散系統的實現 (217)...
4.7.4.二維離散小波變換954.7.5.快速小波變換954.7.6.小波變換的性質964.8.KL變換984.8.1.KL變換984.8.2.KL變換的性質1004.9.希爾伯特變換100...
4.6 離散希爾伯特變換第5章 模擬濾波器5.1 模擬濾波器的基本概念5.2 模擬濾波器的原型設計5.2.1 巴特沃思濾波器5.2.2 切比雪夫濾波器...
5. 6 利用希爾伯特變換研究系統函式的約束特性5. 7 調製與解調5. 8 帶通濾波系統的運用5. 9 從抽樣信號恢復連續時間信號5. 10 脈衝編碼調製(PCM)...
