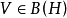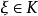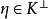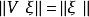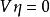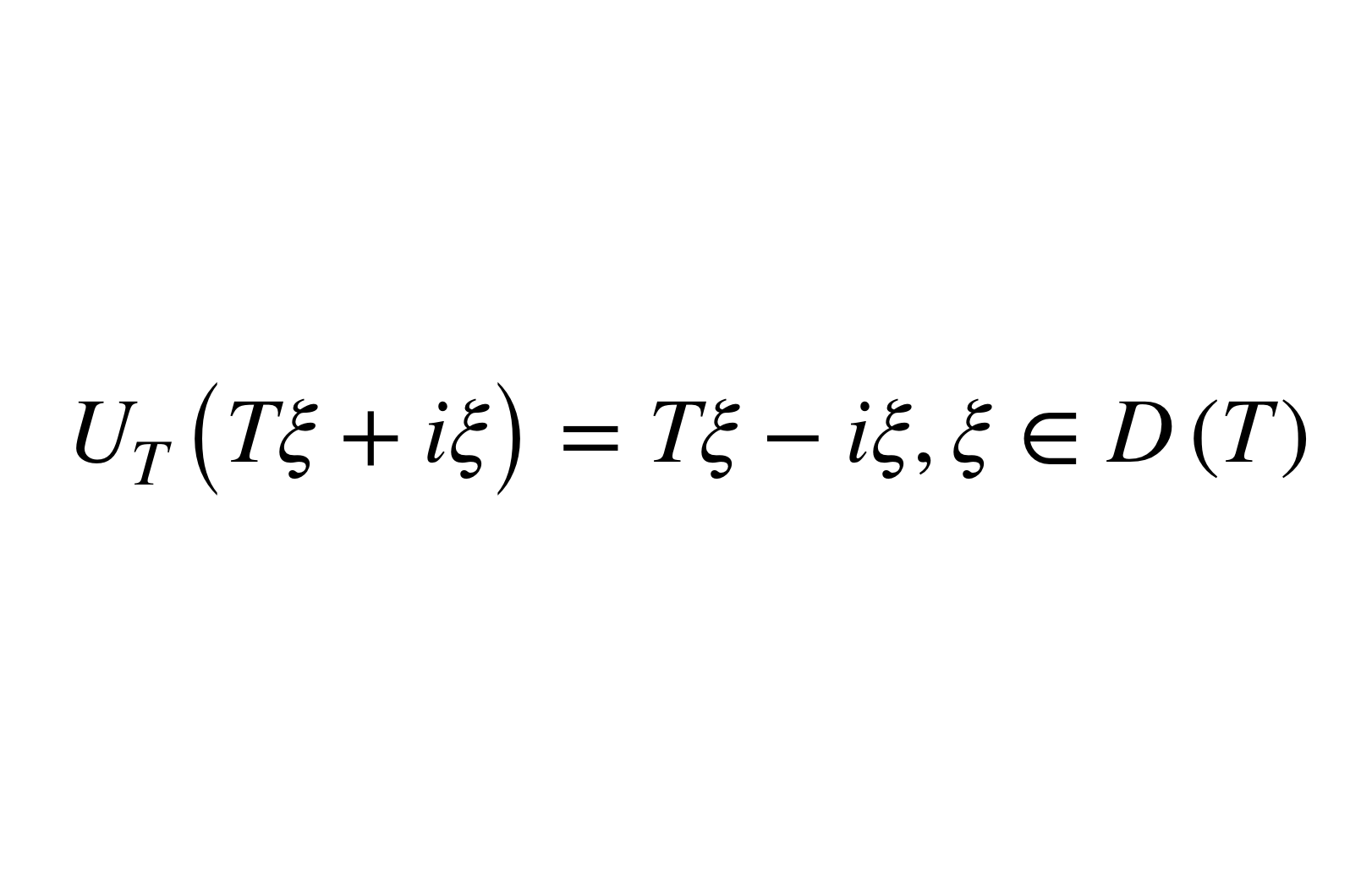凱萊變換是一類特殊的線性變換,所謂凱萊變換是指n維酉空間的酉變換與埃爾米特變換間的一個一一對應。
基本介紹
- 中文名:凱萊變換
- 外文名:Cayley transform
- 適用範圍:數理科學
定義介紹,對稱運算元,部分等距運算元,
定義介紹
凱萊變換在對稱運算元和部分等距離運算元之間建立了一種對應關係。
設𝓗是希爾伯特空間,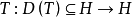 是閉對稱運算元,則
是閉對稱運算元,則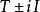 都是單射,且其指域
都是單射,且其指域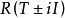 都是𝓗的閉子空間。
都是𝓗的閉子空間。
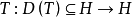
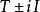
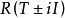
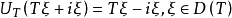
定義了從 到
到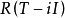 上的等距運算元
上的等距運算元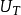 ,稱
,稱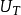 為𝓗的凱萊變換。
為𝓗的凱萊變換。

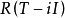
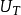
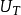
反之,對於𝓗上的部分等距運算元U,若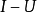 是單射,則
是單射,則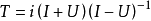 是閉對稱運算元且T的凱萊變換就是U。
是閉對稱運算元且T的凱萊變換就是U。
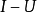
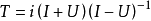
對稱運算元
【symmetric operator】
設T是作用在希爾伯特空間𝓗上的稠定運算元,如果對任意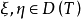 有
有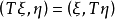 ,亦即
,亦即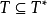 ,則稱T是對稱運算元。每個對稱運算元都有閉的對稱擴張。如果對稱運算元T沒有找到對稱擴張,即若
,則稱T是對稱運算元。每個對稱運算元都有閉的對稱擴張。如果對稱運算元T沒有找到對稱擴張,即若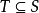 且S是對稱運算元一定有
且S是對稱運算元一定有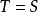 成立時,則稱T是極大對稱(maximally symmetric)。
成立時,則稱T是極大對稱(maximally symmetric)。
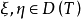
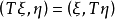
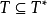
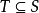
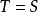
在一定條件下,對稱運算元與等距運算元可通過凱萊變換相互轉化。
部分等距運算元
【partial isometric operator】
設T是希爾伯特空間𝓗的閉子空間,對於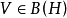 ,如果任意
,如果任意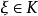 和
和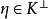 都有
都有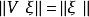 和
和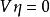 成立,則稱V是以𝓚為初始空間(initial space)以V的值域𝓡(V)為末空間(final space)的部分等距運算元。
成立,則稱V是以𝓚為初始空間(initial space)以V的值域𝓡(V)為末空間(final space)的部分等距運算元。