基本介紹
- 中文名：多變數非線性系統
- 外文名：Multivariable nonlinear systems
- 涉及學科：信息科學
- 又稱：動態非線性系統
- 特徵1：運動特性不能用線性關係描述
- 特徵2：具有多個輸入量或輸出量
非線性系統,意義,區別,多變數系統,特點,優點,二者結合,分析方法,套用和發展,
非線性系統
非線性系統：一個系統,如果其輸出不與其輸入成正比，則它是非線性的。從數學上看，非線性系統的特徵是疊加原理不再成立。疊加原理是指描述系統的方程的兩個解之和仍為其解。疊加原理可以通過兩種方式失效。其一，方程本身是非線性的。其二,方程本身雖然是線性的,但邊界是未知的或運動的。
意義
“線性”與“非線性”是兩個數學名詞。所謂“線性”是指兩個量之間所存在的正比關係。若在直角坐標系上畫出來，則是一條直線。由線性函式關係描述的系統叫線性系統。線上性系統中，部分之和等於整體。描述線性系統的方程遵從疊加原理，即方程的不同解加起來仍然是原方程的解。這是線性系統最本質的特徵之一。“非線性”是指兩個量之間的關係不是“直線”關係，在直角坐標系中呈一條曲線。最簡單的非線性函式是一元二次方程即拋物線方程。簡單地說，一切不是一次的函式關係，如一切高於一次方的多項式函式關係，都是非線性的。由非線性函式關係描述的系統稱為非線性系統。
區別
定性地說，線性關係只有一種，而非線性關係則千變萬化，不勝枚舉。線性是非線性的特例，它是簡單的比例關係，各部分的貢獻是相互獨立的；而非線性是對這種簡單關係的偏離，各部分之間彼此影響，發生耦合作用，這是產生非線性問題的複雜性和多樣性的根本原因。正因為如此，非線性系統中各種因素的獨立性就喪失了：整體不等於部分之和，疊加原理失效，非線性方程的兩個解之和不再是原方程的解。因此，對於非線性問題只能具體問題具體分析。
線性與非線性現象的區別一般還有以下特徵：
（1）在運動形式上，線性現象一般表現為時空中的平滑運動，並可用性能良好的函式關係表示，而非線性現象則表現為從規則運動向不規則運動的轉化和躍變；
（2）線性系統對外界影響的回響平緩、光滑，而非線性系統中參數的極微小變動，在一些關節點上，可以引起系統運動形式的定性改變。在自然界和人類社會中大量存在的相互作用都是非線性的，線性作用只不過是非線性作用在一定條件下的近似。
多變數系統
多變數系統（multivariable systems）是指具有多個輸入量或輸出量的系統，又稱多輸入多輸出系統。
特點
同單變數系統相比，多變數系統的控制複雜得多。在多變數控制系統中，被控對象、測量元件、控制器和執行元件都可能具有一個以上的輸入變數或一個以上的輸出變數。例如汽輪機的蒸汽壓力和轉速控制，石油化工生產中精餾塔的塔頂溫度和塔底溫度控制，渦輪螺旋槳發動機轉速和渦輪進氣溫度的控制等，都是多變數系統的控制問題。多變數系統不同於單變數系統，它的每個輸出量通常都同時受到幾個輸入量的控制和影響，這種現象稱為耦合或交叉影響。交叉影響的存在使多變數系統很可能成為一種條件穩定系統。例如，在調試或運行過程中若增益發生變化或某一元件（例如感測器）斷開或失靈，就可能導致不穩定。這是多變數系統特有的問題。在多變數控制系統的設計中，對於交叉影響的處理，常採用兩種方式：①通過引入適當的附加控制器，實現一個輸入只控制一個輸出，稱為解耦控制（見解耦控制問題）；②協調各個輸入和輸出間的關係，使耦合的存在有利於改善系統的控制性能，稱為協調控制。此外，也可採用其他形式的指標來設計多變數系統的控制器。（見線性系統理論）
優點
1)集中控制便於維護
2)由表頭到單表頭降低數據誤差
多變數系統的結構特點如圖1所示：
圖1
二者結合
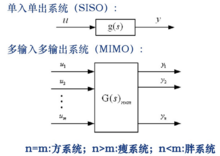
多變數非線性系統（Multivariable nonlinear systems）是指既具有多變數系統的特徵，又具有非線性系統的特徵，即狀態變數和輸出變數相對於輸入變數的運動特性不能用線性關係描述，同時具有多個輸入量或輸出量的控制系統。
線性因果關係的基本屬性是滿足疊加原理（見線性系統）。在非線性控制系統中必定存在非線性元件，但逆命題不一定成立。描述非線性系統的數學模型，按變數是連續的或是離散的，分別為非線性微分方程組或非線性差分方程組。
非線性控制系統的形成基於兩類原因，一是被控系統中包含有不能忽略的非線性因素，二是為提高控制性能或簡化控制系統結構而人為地採用非線性元件。
分析方法
對於非線性系統，建立數學模型的問題要比線性系統困難得多，至於解非線性微分方程，用其解來分析非線性系統的性能，就更加困難了。這是因為除了極特殊的情況外，多數非線性微分方程無法直接求得解析解。所以到目前為止，還沒有一個成熟、通用的方法可以用來分析和設計各種不同的非線性系統，目前研究非線性系統常用的工程近似方法有：
相平面法
相平面法是時域分析法在非線性系統中的推廣套用，通過在相平面上繪製相軌跡，可以求出微分方程在任何初始條件下的解，所得結果比較精確和全面。但對於高於二階的系統，需要討論變數空間中的曲面結構，從而大大增加了工程使用的難度。故相平面法僅適用於一、二階非線性系統的分析。
描述函式法是一種[5]頻域的分析方法，它是線性理論中的頻率法在非線性系統中的推廣套用，其實質是套用諧波線性化的方法，將非線性元件的特性線性化，然後用頻率法的一些結論來研究非線性系統。這種方法不受系統階次的限制，且所得結果也比較符合實際，故得到了廣泛套用。
計算機求解法
用模擬計算機或數字計算機直接求解非線性微分方程，對於分析和設計複雜的非線性系統，幾乎是唯一有效的方法。隨著計算機的廣泛套用，這種方法定會有更大的發展。
應當指出，這些方法主要是解決非線性系統的“分析”問題，而且是以穩定性問題為中心展開的，非線性系統“綜合”方法的研究遠不如穩定性問題的成果，可以說到目前為止還沒有一種簡單而實用的綜合方法，可以用來設計任意的非線性控制系統。
套用和發展
七十年代以後，非線性控制得到比較大的發展，並呈現出多方向發展的趨勢，可歸納為以下三大方面:
基於一些特定模型的非線性控制
在各種特定非線性模型中，以Hammerstein模型和雙線性模型所代表的系統研究得較多.利用這些模型，可以描述眾多的非線性系統，再與一些先進的控制算法相結合以構成非線性控制系統.從目前的研究情況來說，以這些特定模型為基礎構成非線性控制系統的主要算法有:自適應控制、預測控制、內模控制等。這方面目前仍處於發展態勢：一方面各種新的非線性模型尚有推出，同時以這些模型為基礎的先進算法也在發展;另外，從原來的單變數非線性系統拓展到多變數非線性系統.這些非線性控制方法的特點是比較實用且簡單。
八十年代初出現的用微分幾何、微分代數方法來研究非線性系統是非線性系統研究的一大突破.通過變換，非線性系統可以化為線性系統那樣來處理.這種變換不同於經典時期的在某點附近的近似線性化，而是在大範圍(甚至全局的)的精確線性化.運用這些方法，有可能實現非線性系統的大範圍分析綜合。由於這些原因，使得這一領域的研究成為目前控制界的熱門研究課題之一。基於微分幾何的非線性控制方法對於一般的非線性系統尚無能為力。另外，此方法需要有精確的數學模型，這在實際套用中亦受到很大的限制。
智慧型控制在非線性控制中的套用
