基本介紹
- 中文名:偽線性系統
- 外文名:pseudo-linear system
- 分類:計算機 自動控制
- 功能:線性系統的一一種
- 辨識:最小二乘算法
- 相似詞條:線性系統
偽線性系統是指系統經過參數化,得到偽線性回歸模型,其信息向量或信息矩陣包含未知變數(未知內部變數或未知噪聲項)的一類線性系統。偽線性系統的模型是系統輸出或其他變數是參數的線性函式,與系統是否是線性無關,它可以指線性控制系...
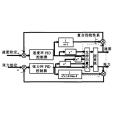
進一步構造神經網路逆系統並與恆壓頻比變頻調速系統串聯複合成偽線性系統,再設計線性閉環調節器實現高性能控制。實驗結果證明了採用神經網路逆控制方法可以使恆壓頻比變頻調速系統獲得優良的運行性能。
8.1.2 偽線性複合系統 8.1.3 逆系統的綜合算法 8.1.4 轉向/制動系統的逆系統解耦 8.2 車輛參數辨識 8.2.1 參數辨識概述 8.2.2 參數辨識的技術發展和研究狀況 8.2.3 車輪側偏特性參數和制動力係數的辨識 8.3 附加的...
6.5 多元線性回歸系統 6.5.1 多元遞推最小二乘辨識算法 6.5.2 M-RLS辨識算法的收斂性 6.5.3 多元隨機梯度辨識算法 6.5.4 M-SG辨識算法的收斂性 6.5.5 仿真試驗 6.6 多元偽線性回歸滑動平均系統 6.6.1 多元遞推增廣...
6.5多元線性回歸系統 6.5.1多元遞推最小二乘辨識算法 6.5,2M—RLS辨識算法的收斂性 6.5.3多元隨機梯度辨識算法 6.5.4M—SG辨識算法的收斂性 6.5.5仿真試驗 6.6多元偽線性回歸滑動平均系統 6.6.1多元遞推增廣最小二乘...
神經網路逆系統方法將神經網路對非線性函式逼近學習能力和逆系統方法的線性化能力相結合,構造出物理可實現的神經網路逆系統,從而實現了對被控系統的大範圍線性化,能夠在無需系統參數的情況下構造出偽線性複合系統,從而將非線性系統的...
3.5.2 系統誤差存在條件下的克拉美羅界40 第Ⅱ部分 無系統誤差條件下的理論與方法篇 第4章 無系統誤差條件下含單重二次等式約束和單輔助變數的 小二乘定位理論與方法:模型a45 4.1 非線性觀測方程的偽線性化模型45 4...
