基本介紹
- 中文名:多變數非線性控制
- 外文名:Multivariable Nonlinear Control
- 涉及學科:信息科學
- 又稱:動態多半量非線性控制
- 特點1:具有多個輸入量或輸出量
- 特點2:運動特性不能用線性關係描述
控制理論
過程控制
解耦理論
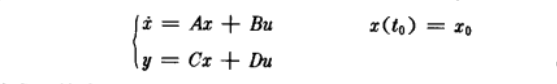
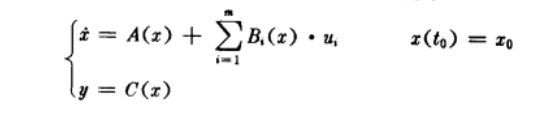
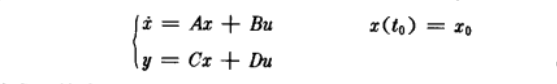
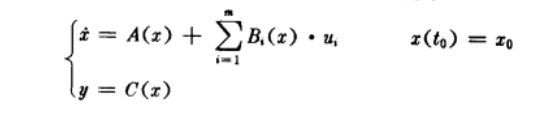
多變數非線性控制(Multivariable Nonlinear Control)是指具有多個輸入量或輸出量的同時狀態變數和輸出變數相對於輸入變數的運動特性不能用線性關係描述的控制方式。控制理論隨著科學技術的發展,人們對...
多變數非線性控制理論 隨著科學技術的發展,人們對實際生產過程的分析要求日益精密,各種較為精確的分析和科學實驗的結果表明,任何一個實際的物理系統都是非線性的。所謂線性只是對非線性的一種簡化或近似,或者說是非線性的一種特例。如...
《多工作點多變數非線性系統魯棒控制》是依託清華大學,由鐘宜生擔任項目負責人的面上項目。項目摘要 本項目將研究一類具有多個工作點的多輸入多輸出非線性系統的單一魯棒控制器的設計問題.所研究的多輸入多輸出受控系統在不同的工作點具有...
《多變數非線性系統自適應控制理論及套用研究》是依託北京航空航天大學,由王陳亮擔任項目負責人的青年科學基金項目。項目摘要 在實際工程中,大多數物理系統都具有多個輸入和多個輸出,並存在不同程度的不確定性。受實際需求的推動,本項目...
適用範圍 《多變數非線性系統的神經網路逆控制方法》主要讀者為從事自動控制的高校師生、研究院所科研人員和工程技術人員,也可供從事其他自動化(如電力系統自動化、機械製造自動化、化工自動化等)工作的高校師生、科技人員參考。
《二維平面電機複雜多變數耦合非線性動力學及控制研究》是依託華中科技大學,由張尚盈擔任項目負責人的青年科學基金項目。中文摘要 針對二維平面電機系統中的複雜非線性和多變數耦合現象,開展動力學建模和控制研究,具體包括:磁場動態邊緣效應...
非線性系統,指的是系統的狀態與輸出變數在外部條件的影響下,不能用線性關係來描述的系統。非線性系統控制是指針對非線性系統而產生的控制方法與理論。基本概念 非線性系統 所謂非線性系統,指的是系統的狀態與輸出變數在外部條件的影響...
偽線性系統的模型是系統輸出或其他變數是參數的線性函式,與系統是否是線性無關,它可以指線性控制系統,也可以指非線性控制系統。因此,偽線性系統都可用最小二乘算法進行辨識。逆系統方法及其分類 逆系統方法是反饋線性化方法中一種比較...
非線性勵磁控制即用非線性的控制方式控制勵磁裝置。從勵磁調節器的控制規律的發展來看,大體經過了四個發展階段:單變數控制階段,多變數控制階段,非線性控制階段,智慧型控制階段。電力系統是一個巨維數的典型動態大系統,它具有強非線性、...
《動框架效應下非線性強耦合磁懸浮轉子穩定控制研究》是依託北京航空航天大學,由湯繼強擔任項目負責人的面上項目。項目摘要 磁懸浮控制力矩陀螺(CMG)是長壽命高精度快回響航天用CMG的前沿發展方向,多變數非線性強耦合是具有強陀螺效應轉子...
第十章 非線性系統Hammerstein模型辨識 10.1 引言 10.2 H-模型線性子系統的辨識 10.3 H-模型非線性增益的辨識 10.4 H-模型的m3序列辨識法 10.5 計算結果與分析 10.6 結論 第十一章 多變數控制系統Fisher信息矩陣結構 11.1 ...
非線性控制系統理論 非線性控制系統理論(nonlinear control system theory)是1990年公布的自動化科學技術名詞。公布時間 1990年,經全國科學技術名詞審定委員會審定發布。出處 《自動化名詞》第一版。
這一方面是由於理論的發展,特別是非線性系統幾何理論的誕生,為實際套用提供了可能性;另一方面,則來自實踐的需要,特別是航空、航天等高新技術對精度要求越來越高,使傳統的近似方法無法滿足。事實上,非線性控制系統的發展幾乎是與線性...
書 名: 非線性系統理論 作 者:方勇純 出版社: 清華大學出版社 出版時間: 2009年05月 ISBN: 9787302193036 開本: 16開 定價: 22元 內容介紹 《非線性系統理論》適用對象為高等院校自動化專業研究生,以及從事非線性控制系統分析...
針對這些技術瓶頸,本項目著重研究如下三方面課題:(1)研究任意干擾相對階多變數非線性系統的主動抗干擾控制問題;(2)探索複雜結構不匹配干擾系統的主動抗干擾控制方法;(3)提出不匹配受擾非線性系統的有限時間主動抗干擾控制策略。該...
多變數非線性系統的自適應模糊控制設計方法與穩定性分析;多變數非線性系統的自適應輸出反饋模糊控制設計方法與穩定性分析;非線性大系統的自適應分散模糊控制設計方法與穩定性分析;多變數非線性系統的自適應模糊辨識、模糊控制設計方法與...
第4章 非線性系統的自適應模糊滑模控制 第5章 基於模糊滑模的非線性系統自適應模糊控制 第6章 非線性系統的自適應輸出反饋模糊控制 第7章 基於高增益觀測器的非線性系統自適應輸出反饋模糊控制 第8章 多變數非線性系統的自適應模糊...
0.3.2 非線性隨機系統的穩定性 4 0.3.3 非線性狀態約束系統的穩定性 4 0.4 非線性小增益定理 5 參考文獻 6 第1章 非線性嚴格反饋系統智慧型自適應狀態反饋控制 7 1.1 非線性系統模糊自適應狀態反饋控制 7 1.1.1 系統模型...
通過對輸入和狀態變數的變換把非線性系統近似線性化,雖然便於人們更方便,更簡單的理解系統的特點,但是難以描繪出原系統的非線性特徵,線性化後的系統不能很好的體現實際系統的非線性特徵。上個世紀以來,非線性控制理論有了巨大的拓展。...
通過對輸入和狀態變數的變換把非線性系統近似線性化,雖然便於人們更方便,更簡單的理解系統的特點,但是難以描繪出原系統的非線性特徵,線性化後的系統不能很好的體現實際系統的非線性特徵。上個世紀以來,非線性控制理論有了巨大的拓展。...
