基本介紹
- 中文名：函式的奇偶性
- 外文名：odevity of a function
- 學科：數學
- 地位：函式的基本性質
相關詞條
- 函式的奇偶性
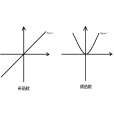
函式的奇偶性是指在關於原點的對稱點的函式值相等，是函式的基本性質之一，指其圖象有某種對稱性的一元函式。定義在對稱區間1= (-a,a)或[-a,a](或數軸上關於原點對稱的點集)上的(一元)實值函式y=f (x)。函式簡介 函式的奇偶...
- 偶函式
“偶函式”之名顯然源於冪函式的指數或指數分子的奇偶性：指數為偶數的冪函式為偶函式， 指數為奇數的冪函式為奇函式。《無窮分析引論》中的奇、偶函式概念 1748年,歐拉出版他的數學名著《無窮分析引論》，將函式確立為分析學的最基本...
- 函式性質
函式的幾種特性 ①有界性 單調函式②單調性③奇偶性 ④周期性 公式一: 設α為任意角,終邊相同的角的同一三角函式的值相等: sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα ...
- 函式的奇偶性微課
《函式的奇偶性微課》是安丘市第一中學提供的微課課程，主講老師是李鳳民。課程簡介 1、利用奇偶函式的定義判斷函式的奇偶性，並歸納求解步驟。2、利用奇偶函式的性質解決實際問題。設計思路 函式的奇偶性是函式的一個非常重要的性質，函式...
- 一次函式和二次函式
奇偶性 當b≠0時 非奇非偶; 當b=0時 奇函式 函式值的改變數與相應自變數的改變數成正比。二次函式 解析式 一般式：y=ax^2+bx+c(a≠0)頂點式：y=a（x-m）2+n（a≠0），其中（m、n）為拋物線的頂點 兩點式：y=...
- 函式的性態及套用
具體包括：函式的定義；函式的單調性；函式的奇偶性；函式的周期性；函式的可導性等。函式是高中數學的核心概念，函式的學習貫穿於整個高中階段，在高中數學大部分章節中都涉及函式或者函式的思想方法。從某種意義上可以說，作為高中基礎的...
- 雙曲餘弦函式
函式性質 定義域與值域 雙曲餘弦函式的定義域為 。值域為[1, )。當x=0時，取到最小值1。奇偶性 雙曲餘弦函式在定義域內是偶函式。可以證明。取x的負值。又得：根據加法交換律，可得出 。根據偶函式的定義，可知該函式是偶...
- 七次函式
七次函式不具有一般性質，因此研究七次函式需要分類討論。奇偶性 一般地，當六次項及以下偶次項的係數為0，函式為奇函式。（如圖1）反之，則函式為非奇非偶函式。單調性 七次函式單調性較為複雜，一般通過求導方法確定導函式的零點，再...
- 高中數學經典題型全解析:預備知識與函式
本書共五篇，分別是預備知識、函式的概念和性質、指數函式和對數函式、函式套用以及專題提升。本書對集合、充要條件、基本不等式、一元二次不等式、函式、函式的單調性、函式的奇偶性、指數函式、對數函式、二分法等重要概念的形成過程，...
- 冪函式
一般地，y=x（α為常數）的函式，即以底數為自變數，冪為因變數，指數為常量的函式稱為冪函式。例如函式y=x⁰ 、y=x¹、y=x²、y=x（註：y=x=1/x、y=x⁰時x≠0）等都是冪函式。定義域和值域及其奇偶性 冪函式...
- 對數函式
對數函式是6類基本初等函式之一。其中對數的定義:如果ax =N(a>0,且a≠1),那么數x叫做以a為底N的對數,記作x=logaN,讀作以a為底N的對數,其中a叫做對數的底數,N叫做真數。一般地,函式y=logaX(a>0,且a≠1)叫做對數函式,也...
- 六次函式
方程中a、b、c、d、e、f分別為六次、五次、四次、三次、二次、一次項係數，g為常數，a≠0.在實際中，一般不使用此函式。函式性質 定義域：R 值域：a>0時，有最小值，無最大值。a 單調性：根據函式解析式而變換。奇偶性：...
- 基本初等函式
冪函式的圖象一定會出現在第一象限內，一定不會出現在第四象限，至於是否出現在第二、三象限內，要看函式的奇偶性；冪函式的圖象最多只能同時出現在兩個象限內；如果冪函式圖象與坐標軸相交，則交點一定是原點。冪函式取正值 當α>0...
- 分段函式
所以原函式的值域為：（1）當-2≤a （2）當0≤a≤2時,為(-∞,-a)∪[0,4]；（3）當a>2時,為(-∞,-a)∪[0,a2]求分段函式的值域的方法：分別求出各段函式在其定義區間的值域，再取它們的並集即可。函式的奇偶性 例4...
- 二次函式
上是增函式，在 上是減函式；拋物線的開口向下；函式的值域是 。當 時，拋物線的對稱軸是y軸，這時，函式是偶函式，解析式變形為y=ax²+c(a≠0)。8.定義域：R 9.值域：當a>0時，值域是 ；當a 。奇偶性：當b=0...
- 餘割函式
1、在三角函式定義中，cscα=r/y。2、餘割函式與正弦互為倒數：cscx=1/sinx。3、定義域：{x|x≠kπ，k∈Z}。4、值域：{y|y≥1或y≤-1}。5、周期性：最小正周期為2π。6、奇偶性：奇函式。7、圖像漸近線：x=kπ，k...
- 微積分拾階(1)
我們可以看到，這個定義是與有界性的定義不同的一種定義方式，就是我們一般可以直接套用這個定義來證明某個函式的奇偶性，這種定義方式就是屬於構造性的定義方式。也就是直接給出了符合定義的對於如何構造出來。在今後的學習當中，我們應該...
- 考點同步解讀:高中數學1
1.3.2奇偶性 考點1函式奇偶性的概念 導師·導學準確理解函式奇偶性的概念 梳理·歸納奇（偶）函式的若干問題 梳理·歸納判斷函式奇偶性的常用方法 考點2函式奇偶性的簡單套用 拓展·研討奇偶性的妙用 考點3奇偶函式圖象的對稱性 導師·...
- cth
奇偶性 奇函式 導函式 (cthx)'=(ehx)^2 運算性質 th (x±y)=(cthxcthy±1)/(cthx±cthy)th (x±y)=(1±thxthy)/(thx±thy)th2x=cthx-thx/2 證明 th(x±y)=sh(x±y)/ch(x±y)=shxshy±chxchy/shxchy±...
- 高等數學——新證明法講解
第二節 函式的概念 習題1—2 第三節 函式的性質 一、函式的有界性 二、函式的單調性 三、函式的奇偶性 四、函式的周期性 習題1—3 第四節 反函式與複合函式 一、反函式 二、複合函式 ...
- coth
雙曲餘切函式是雙曲函式中的一個函式，其是雙曲正切函式的倒數。定義域和值域 函式：y=coth x；定義域：{ x | x≠0 }，值域：{ y | |y|大於1}。奇偶性：y=coth x 是一個奇函式，其函式圖像分為兩支，分別在Ⅰ、Ⅲ象限...
- 微積分1
第1章 函式 1.1 函式概念 1.1.1 函式的定義 1.1.2 函式的例子 習題1 1.2 函式的初等性質 1.2.1 函式的奇偶性 1.2.2 函式的增減性 1.2.3 函式的周期性 1.2.4 函式的有界性 1.2.5 函式的凸凹性 習題2 1.3 ...
- 對應法則
在確定兩個函式是否為同一函式時，定義域和值域都相同不一定就是同一函式，對應法則f為關鍵要素。可以運用化學的知識理解y相當於生成物，f相當於反應條件或者是催化劑把反應物x變為y。由函式奇偶性的定義我們知道，判斷函式的奇偶性，...
- SECH
奇偶性 偶函式 導函式 (sech)'=(1/chx)'=(chx)'/ch^2x=-thxsechx 運算性質 運算性質 sech(x±y)=secxsecy/1±thxthy=cscxcscy/cthxcthy±1 sech2x=1/sh^2x+ch^2x=sech^2x/th^2x+1=csch^2x/cth^2x+1 1/sh^...
- 創新升級版重難點手冊高中數學1 必修 RJA(第六版)
考向4 函式單調性的創新問題 1.3.2 奇偶性 要點1 函式的奇偶性 要點2 奇（偶）函式圖象的特徵 考法1 函式奇偶性的判定方法 考法2 函式的奇偶性與單調性的關係 考法3 函式奇偶性的套用 誤區1 忽視函式的定義域 誤區2 忽視...
- 餘割
函式 記為：y=cscα=1/sinα；函式性質：1、定義域：{x|x≠kπ，k∈Z} 2、值域：{y|y≤-1或y≥1} 3、奇偶性：奇函式 4、周期性：最小正周期為2π 圖像漸近線為：x=kπ ，k∈Z 性質 1、在三角函式定義中，cscα=...
- 高中數理化生公式定律&要點透析
函式定義域的求法 函式值域的求法 區間 函式的表示法 分段函式 映射 原象與象 一一映射 映射與函式的關係 3.函式的基本性質 函式的單調性 判斷函式單調性的方法 有關函式單調性的結論 函式的最大（小）值 函式的奇偶性 有關函式...
- 最新考研數學(三)常考題型解題方法技巧歸納
1.1 函式 1.1.1 求幾類函式的表達式 題型一 已知函式，求其反函式的表達式 題型二 求分段函式的複合函式 1.1.2 判別（證明）幾類函式的奇偶性 題型一 判別經四則運算後的函式的奇偶性 題型二 判別自變數帶相反...
- 對數曲線
值域：實數集R，顯然對數函式無界；定點：對數函式的函式圖像恆過定點（1，0）；單調性：a>1時，在定義域上為單調增函式；0 奇偶性：非奇非偶函式 周期性：不是周期函式 對稱性：無 最值：無 零點：x=1 注意：負數和0沒有對數...
