基本介紹
- 中文名:奇函式
- 外文名:odd function
- 形式:f(-x)= - f(x)
- 特點:定義域關於原點對稱
定義


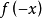
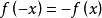
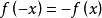


性質
特點








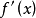


發展
歐拉最早定義
歐拉拓展概念
歐拉的大困惑




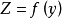



後世發展演變
例子
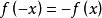








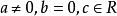




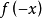
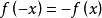
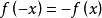










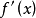






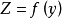



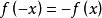








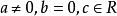

奇函式是指對於一個定義域關於原點對稱的函式f(x)的定義域內任意一個x,都有f(-x)= - f(x),那么函式f(x)就叫做奇函式(odd function)。1727年,年輕的...
函式的奇偶性是指在關於原點的對稱點的函式值相等。是函式的基本性質之一,指其圖象有某種對稱性的一元函式.定義在對稱區間1= (-a,a)或[-a,a}(或數軸上...
赫維賽德函式單位階躍函式、階躍函式或開關函式, 它被用在電路的研究中,用來表示電閘接通的瞬時電路中電流或電壓的突然變動。斜坡函式,它是赫維賽德函式的積分形式,...
對勾函式是一種類似於反比例函式的一般雙曲函式,是形如f(x)=ax+b/x(a×b>0)的函式。由圖像得名,又被稱為“雙勾函式”、“勾函式”、"對號函式"、“...
一般地,形如函式,稱為七次函式。在實際的數學套用中出現的很少。...... 一般地,當六次項及以下偶次項的係數為0(即函式屬於冪函式),函式為奇函式。(如圖) 七...
共軛反對稱函式(conjugate antisymmetric function)是指具有共軛反對稱特性的一種頻譜函式,序列的傅立葉變換,通常稱為序列的頻譜函式,如果頻譜函式X(ejω)滿足X(e...
解析函式奇點,數學概念,即函式不解析的點。...... 解析函式奇點(singular point of analytic function)函式不解析的點.若函式f(z)在點z=u 的任一鄰域內不能展...
奇偶性是函式的基本性質之一。一般地,如果對於函式f(x)的定義域內任意一個x,都有f(-x)=f(x),那么函式f(x)就叫偶函式。一般地,如果對於函式f(x)的定義...
在直角三角形中,某銳角的相鄰直角邊和相對直角邊的比,叫做該銳角的餘切。餘切與正切互為倒數,用“cot+角度”表示。餘切函式的圖象由一些隔離的分支組成(如圖)。...
記作cscx.它與正弦的比值表達式互為倒數。餘割的函式圖像為奇函式,且為周期函式。 [1] 餘割函式 記為:y=cscα=1/sinα;函式性質:...
原點對稱是數學中的一種幾何現象,原點是X軸與Y軸的交點。奇函式的任何一個點都有對稱點,直角坐標繫上一點(x,y)關於原點對稱的點為(-x,-y)。...
在信號系統分析中,經常要遇到函式本身有不連續點(跳變點)或其導數有不連續點的情況,這類函式稱為奇異函式或奇異信號。...
指數函式的一般形式為y=a^x(a>0且不=1) ,函式圖形上凹,a大於1,則指數函式單調遞增;a小於1大於0,則為單調遞減的函式。指數函式既不是奇函式也不是偶函式...
