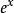七次函式

一般地，形如函式，稱為七次函式。在實際的數學套用中出現的很少。

基本介紹

• 中文名：七次函式
• 外文名：Seven-order Function
• 套用學科：數學
• 定義域：R
• 值域：R
• 奇偶性：分類討論
• 單調性：分類討論
• 零點個數：分類討論，一般無解析解

概念

一般地，形如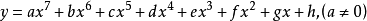

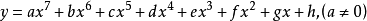
的函式，我們稱之為七次函式。

七次函式屬於高次函式，其中x為自變數，y為x的函式。

對於七次函式，零點沒有一般解法，由於太過複雜且實用性不高，一般較少出現在數學套用領域。

儘管如此，對不同函式的深入研究，可以增長我們的見識，鍛鍊思維，提高數學觀念，學習新知，體驗數形結合的樂趣。

另外，在求函式的冪級數展開時，可能會在高階要求下出現。

性質

七次函式不具有一般性質，因此研究七次函式需要分類討論。

奇偶性

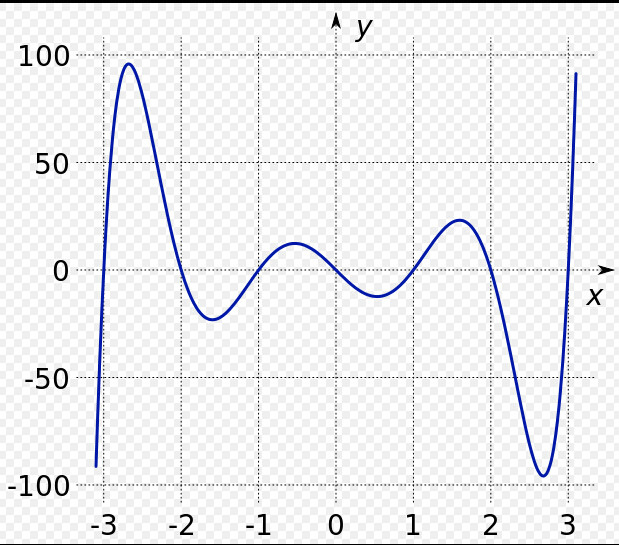
一般地，當六次項及以下偶次項的係數為0（即函式屬於冪函式），函式為奇函式。（如圖）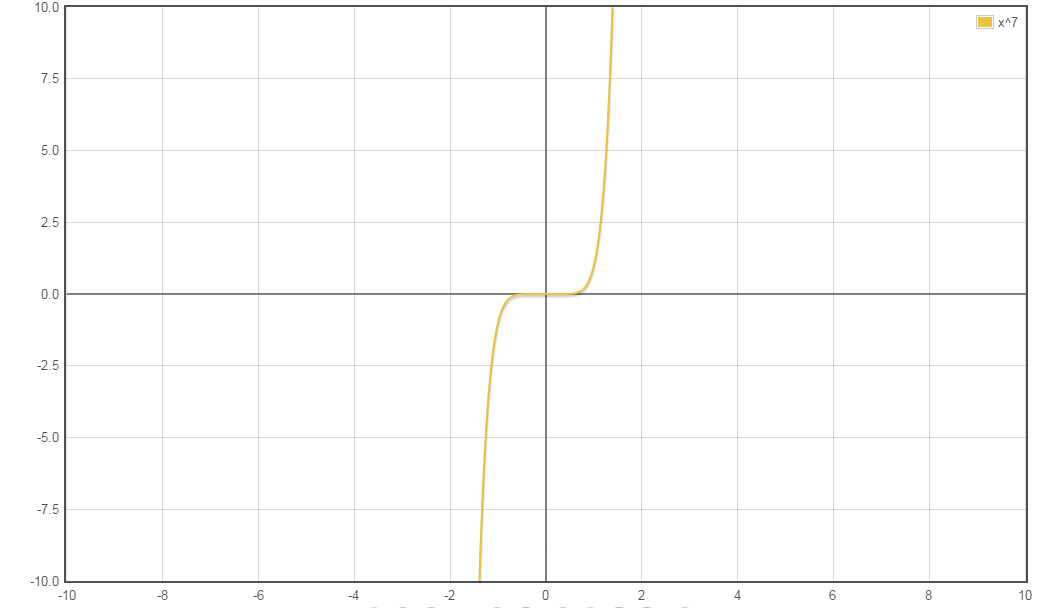

七次函式的一般形式

反之，則函式為非奇非偶函式。

單調性

七次函式單調性較為複雜，一般通過求導方法確定導函式的零點，再做出判斷。。但五次以上的高次方程已近不能解出解析解了，所以一般套用是最多選取一定精度範圍的近似零點。

特殊點

當x=0時，過點（0，h)。

當七次函式為冪函式，過點（0.0）

當x∈R時，無特殊點。

定義域

R

值域

R

套用

七次函式是高次函式，凡是超過五次以上的多項式和的函式，都稱作高次函式。一般都不會在數學實際套用中出現，有可能會出現在函式的高階冪級數展開，例如：

對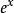 展開至七次，即：

是 泰勒級數的展開，這裡使用了帶Peano（佩亞諾）餘項的形式。

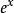
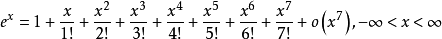
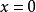或者是 在 處的展開

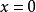
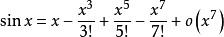
但是，這些近似都要求過高，一般只需要去前幾項，對於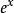 ，只需要展開到四階。另外，還有其他冪級數的形式例如拉格朗日插值多項式，又稱作拉格朗日插值公式。