基本介紹
- 中文名:雙曲餘弦函式
- 外文名:hyperbolic cosine
- 領域:數學
- 字母簡寫:cosh
- 性質:6種
- 套用:高等數學
- 範疇:雙曲函式
函式定義

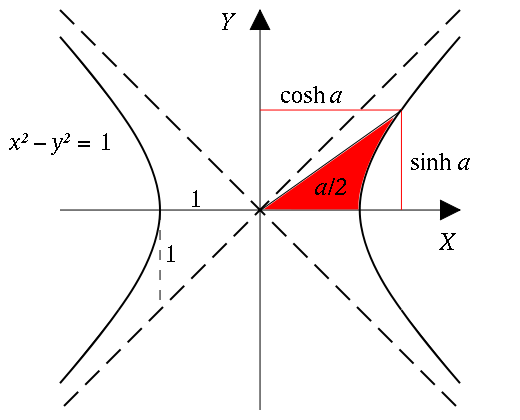

函式性質
定義域與值域


奇偶性



單調性









周期性
凹凸性





套用領域
導數


不定積分



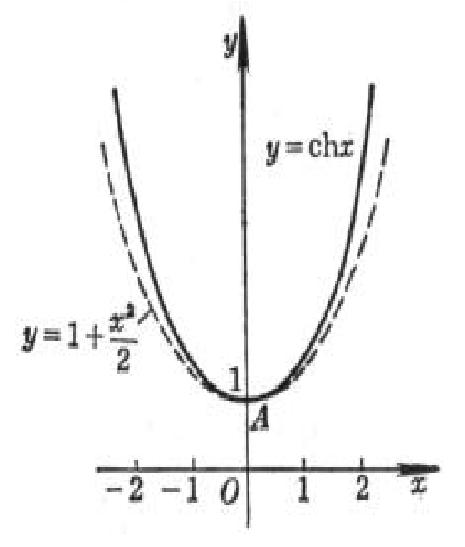
泰勒展開式


反函式






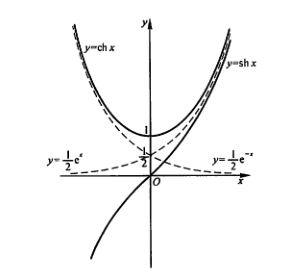
函式圖像

相關公式








































































在數學中,雙曲函式是一類與常見的三角函式(也叫圓函式)類似的函式。最基本的雙曲函式是雙曲正弦函式sinh和雙曲餘弦函式cosh,從它們可以導出雙曲正切函式tanh等,其推導也類似於三角函式的推導。雙曲函式的反函式稱為反雙曲函式。雙...
稱形如 f(x)=csc x的函式為餘割函式,它的定義域為 ,值域為 ,最小正周期為 。 基本函式其它常見函式 編輯 語音 基本函式雙曲函式 雙曲正弦函式:雙曲餘弦函式:雙曲正切函式:基本函式反雙曲函式 反雙曲正弦函式:反...
還有一系列雙曲函式也是初等函式,如sinh的名稱是雙曲正弦或超正弦,cosh是雙曲餘弦或超餘弦,tanh是雙曲正切,coth是雙曲餘切,sech是雙曲正割,csch是雙曲餘割。初等函式在其定義區間內一定連續。一個初等函式,除了可以用初等解析式...
另外,以三角函式為模版,可以定義一類相似的函式,叫做雙曲函式。常見的雙曲函式也被稱為雙曲正弦函式、雙曲餘弦函式等等。三角函式(也叫做圓函式)是角的函式;它們在研究三角形和建模周期現象和許多其他套用中是很重要的。三角函式...
函式定義 一組預定義的函式,這些函式作為 Transact-SQL 和多維表達式 (MDX) 語言的部分而提供。JavaScript 1.數學函式 abs 方法 返回一個數的絕對值。acos 方法 返回一個數的反餘弦。anchor 方法 在對象的指定文本兩端加上一個帶 ...
0 以10為底的對數稱為常用對數 ,簡記為lgx 。在科學技術中普遍使用的是以e為底的對數,即自然對數,記作lnx。④三角函式 ⑤反三角函式 ⑥雙曲函式:雙曲正弦 ,雙曲餘弦 ,雙曲正切 / ,雙曲餘切 / 。
acos -- 反餘弦 acosh -- 反雙曲餘弦 asin -- 反正弦 asinh -- 反雙曲正弦 atan2 -- 兩個參數的反正切 atan -- 反正切 atanh -- 反雙曲正切 base_convert -- 在任意進制之間轉換數字 bindec -- 二進制轉換為十進制 ceil...
函式圖像如下 Tanh函式 Tanh是雙曲函式中的一個,Tanh()為雙曲正切。在數學中,雙曲正切“Tanh”是由基本雙曲函式雙曲正弦和雙曲餘弦推導而來。公式如下 函式圖像如下 ReLU函式 Relu激活函式(The Rectified Linear Unit),用於隱層神...
1.5 asin、asinl函式:反正弦函式 1.6 atan函式:反正切函式 1.7 atan2、atan2l函式:計算Y/X的反正切值 1.8 cabs函式:計算複數的模 1.9 ceil函式:向上取整 1.10 cos函式:餘弦函式 1.11 cosh函式:雙曲餘弦函式 1.12...
雙曲線函式 《雙曲線函式》是1936年上海商務印書館出版的圖書,作者是徐玉相。書前冠:序言。—教本 摘要
毛羅利科早於1558年已採用三角函式符號(Signs for trigonometric functions), 但當時並無函式概念,於是只稱作三角線( trigonometric lines)。他以sinus 1m arcus 表示正弦,以sinus 2m arcus表示餘弦。來歷 正弦是最重要也是最古老的一...
最基本的雙曲函式是雙曲正弦函式 sinh 和雙曲餘弦函式 cosh,從它們可以導出雙曲正切函式 tanh 等,其推導也類似於三角函式的推導。雙曲函式的反函式稱為反雙曲函式。雙曲函式的定義域是實數,其自變數的值叫做雙曲角。雙曲函式出現...
適當選擇坐標系後,懸鏈線的方程是一個雙曲餘弦函式,其標準方程為:y=a cosh(x/a),其中,a為曲線頂點到橫坐標軸的距離。歷史發展 問題的起源 達·文西不僅是義大利的著名畫家,他畫的《蒙娜麗莎》帶給了世界永恆的微笑,而且他還是...
雙曲餘弦函式:;反雙曲餘弦函式:雙曲正切函式:;反雙曲正切函式:雙曲餘切函式:反雙曲餘切函式:分段函式。我們在實際問題中會經常遇到一種特殊形式的函式,它不屬於初等函式,而是由一些在不同的定義域區間定義的初等函式組合起來的...
懸鏈線光學是現代光學的一個分支,研究利用懸鏈線函式描述亞波長尺度的光學效應。懸鏈線函式可分為兩類,一類是雙曲餘弦函式(也稱為普通懸鏈線),可描述兩列相向傳播的倏逝波干涉形成的電場強度分布;另一類是對數餘弦函式(又稱為等強度...
適當選擇坐標系後,懸鏈線的方程是一個雙曲餘弦函式。它在數學中和工程中都有很重要的套用。懸鏈線圍繞其水平準線旋轉而成的曲面稱為懸鏈面。懸鏈面是微分幾何中很重要的一種曲面,它的重要性在於它既是不尋常的極小曲面,又是旋轉曲面...
99任意銳角的正弦值等於它的餘角的餘弦值,任意銳角的餘弦值等於它的餘角的正弦值 100任意銳角的正切值等於它的餘角的餘切值,任意銳角的餘切值等於它的餘角的正切值 圓 101圓是定點的距離等於定長的點的集合 102圓的內部可以看作是...
cmath是c++語言中的標準庫頭檔案。其中的 “c” 表示其中的函式是來自 C標準庫,“math”表示為數學常用庫函式。常用函式 cmath 頭檔案中包含了對以下常用數學函式的說明:以及:log,log10;sin;cos;tan等函式。C語言提供了以下的...
。這是雙曲餘弦函式。約翰對解決懸鏈線問題大為得意。在此基礎上,約翰與雅格布還在1691—1692年間解決了懸掛著的變密度非彈性軟繩、等厚度的彈性繩、以及在每一點上的作用力都指向一個固定中心的細繩所形成的形狀的問題。約翰和萊布尼茲...
式中ch(·)、sh(·)為雙曲餘弦函式與雙曲正弦函式。線性律 假定紅、藍兩軍各自使用武器(如火炮)對對方實施遠距離間接瞄準射擊,火力集中在已知對方戰鬥單位的集結地區,該區域的大小與對方部隊的數量無關。此時一方的損傷率與對方向其...
的原函式,當 時為零。我們有:注意到 是sinc函式,也是第零個球貝塞爾函式。2.餘弦積分 餘弦積分定義為:兩者將的關係式為:其中 是歐拉-馬歇羅尼常數。 是 的原函式,當 時為零。我們有:3.雙曲正弦積分 4.雙曲餘弦積...
②梁的振動矩形截面梁作橫向振動的振型由正弦、餘弦、雙曲正弦和雙曲餘弦函式線性組合而成,其固有頻率為:式中 為係數;l為梁長;h為梁截面沿振動方向的高度; 為梁的材料密度;E為梁的彈性模量(見材料的力學性能)。上式表示...
