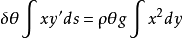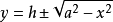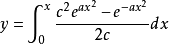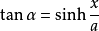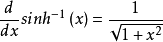歷史發展
問題的起源
達·文西不僅是義大利的著名畫家,他畫的《蒙娜麗莎》帶給了世界永恆的微笑,而且他還是數學家、物理學家和機械工程師,他學識淵博,多才多藝,幾乎在每個領域都有他的貢獻,他還是數學上第一個使用加、減符號的人,他甚至認為:“在科學上,凡是用不上數學的地方,凡是與數學沒有交融的地方,都是不可靠的”。他本人在創作《蒙娜麗莎》時,認真地研究了主人公的心理,做了各種精確的數學計算,來確定人物的比例結構,以及半身人像與背景間關係的構圖問題。當我們欣賞著他的《抱銀貂的女人》中脖頸上懸掛的黑色珍珠項鍊時,我們注意的是項鍊與女人相互映襯的美與光澤,而不會像達·文西那樣去苦苦思索這樣一個問題:固定項鍊的兩端,使其在重力的作用下自然下垂,那么項鍊所形成的曲線是什麼?

這就是著名的懸鏈線問題,達文西還沒有找到答案就去世了。
發展
從外表上看,懸鏈線真的很像拋物線。荷蘭物理學家惠更斯用物理方法證明了這條曲線不是拋物線,但到底是什麼,他一時也求不出來。直到幾十年後,雅各布·伯努利再次提出這個問題。
解決問題
與達文西的時代時隔170年,久負盛名的雅各布·伯努利在一篇論文中提出了確定懸鏈線性質(即方程)的問題。實際上,該問題存在多年且一直被人研究。伽利略就曾推測過懸鏈線是一條拋物線,但問題一直懸而未決。雅各布覺得,套用奇妙的微積分新方法也許可以解決這一問題。
但遺憾的是,面對這個苦惱的難題,他沒有絲毫進展。一年後,雅各布的努力還是沒有結果,可他卻懊惱地看到他的弟弟約翰·伯努利發表了這個問題的正確答案。而自命不凡的約翰,卻幾乎不可能算是一個謙和的勝利者,因為他後來回憶說:
我哥哥的努力沒有成功;而我卻幸運得很,因為我發現了全面解開這道難題的技巧(我這樣說並非自誇,我為什麼要隱瞞真相呢?)……沒錯,為研究這道題,我整整一晚沒有休息……不過第二天早晨,我就滿懷欣喜地去見哥哥,他還在苦思這道難題,但毫無進展。他像伽利略一樣,始終以為懸鏈線是一條拋物線。停下!停下!我對他說,不要再折磨自己去證明懸鏈線是拋物線了,因為這是完全錯誤的。
可笑的是,約翰成功地解出這道難題,僅僅犧牲了“整整一晚”的休息時間,而雅各布卻已經與這道題持續搏鬥了整整一年,這實在是一種“奇恥大辱”。
等高懸鏈線
標準方程
其中,a為常數,是曲線頂點到橫坐標軸的距離。
表達式的證明
如右圖,設最低點A處受水平向左的拉力H,右懸掛點處表示為C點,在AC弧線區段任意取一段設為B點,則B受一個斜向上的拉力T,設T和水平方向夾角為θ,AB段繩子的質量為m,顯然B點受力平衡,進行
受力分析有:
m=σs ,其中s是右段AB繩子的長度,σ是繩子線密度,即單位長度繩子的質量。代入得微分方程
(式1);再利用勾股定理
得到式(2):
將(2)式代入(1)式得式(3):
為了將積分符號去掉,對上式兩邊對x求導:
接下來變數分離並兩端進行積分:
(注意,指數-1表示的是反函式,而不是倒數。)
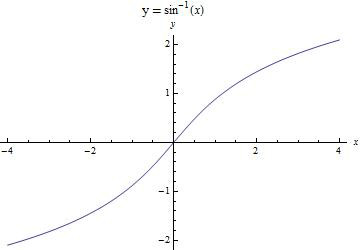 反雙曲正弦的部分圖像
反雙曲正弦的部分圖像下面確定C的值。顯然,當x=0時,y'=0,即p=0,所以將該初值條件代入我們得到的解,因為
,解得C=0。下面給出反雙曲正弦的圖像以加強直觀認識。
然後利用反函式的性質,在(4)式的兩邊取雙曲正弦:
對上式變數分析並積分:
於是得到最終的解:
上式中的C一般保留,它會隨著坐標系選擇的不同而取不同的值。
懸流體方程
以下是不同a的曲線族。方程原理同懸鏈線一樣。不同的是其表面張力分量必須等於懸掛部分的重力。
垂直方向的流體必須考慮懸流體部分,此部分不是自由流動的流體,其完全受表面張力作用。
如果張力僅僅能夠維持自身旋轉體重量時,摩擦阻力不考慮。
(2)垂直管道中,或者空氣柱內,摩擦阻力與y正比,反重力方向,則微分方程為:
此類如同自然水管龍頭的低速流體,但是它需要一個水平方向的張力作用,大小等於ky,第一類與二類均需要。
(2)水平轉換張力球,水龍頭如果開到很小,會發現,在最底端,水是以一個一個的小球發出,而這個小球就是張力球,水按照一定頻率從懸流體中流出,而不是連續的流體,與量子力學基本相通,微分方程如下:
懸膜殼或者懸流體膜
利用積分程式繪圖如下:
工程中的套用
懸索橋、
雙曲拱橋、
架空電纜、雙曲拱壩都用到懸鏈線的原理。 在工程中有一種套用,
a稱作懸鏈係數。如果我們改變公式的寫法,會給工程套用帶來很大幫助,公式及圖像如下:
還有以下幾個公式,可能也有用:
其中L是曲線中某點到0點的鏈索長度,α是該點的正切角,F0是0點處的水平張力,γ是鏈索的單位重量。利用上述公式即能計算出任意點的張力。
相關公式

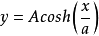
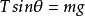








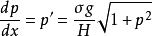
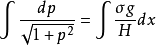
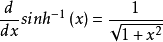
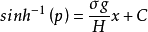
 反雙曲正弦的部分圖像
反雙曲正弦的部分圖像