基本介紹
- 中文名:雙曲正切函式
- 外文名:hyperbolic tangent function, tanh
- 類型:實變函式,雙曲函式
- 學科:數學
定義

運算
導數

積分


泰勒展開
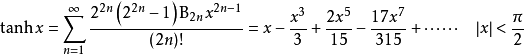

反函式
 反雙曲正切函式的圖像
反雙曲正切函式的圖像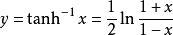
與其他雙曲函式的關係
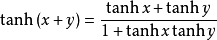


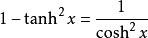
性質
有界性



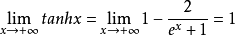



奇偶性

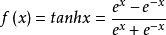
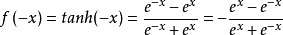
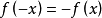
周期性
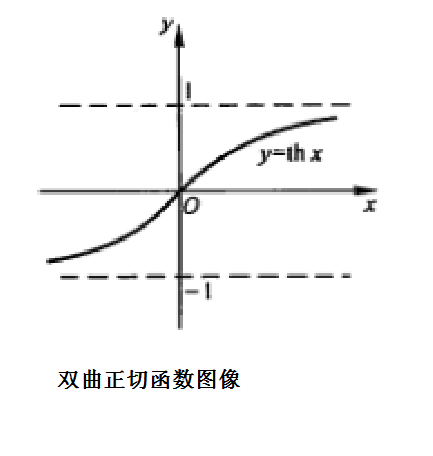 雙曲正切函式的圖像
雙曲正切函式的圖像單調性



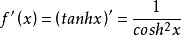

凹凸性
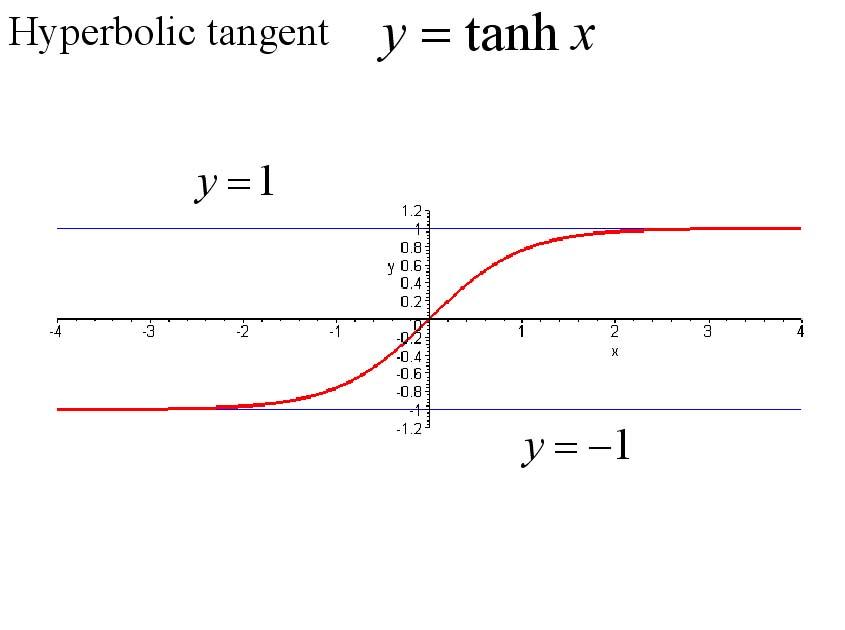 雙曲正切函式的圖像
雙曲正切函式的圖像



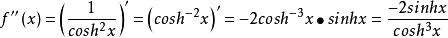





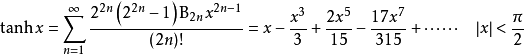

 反雙曲正切函式的圖像
反雙曲正切函式的圖像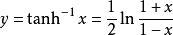
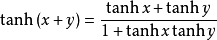


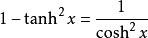



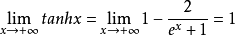




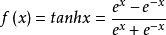
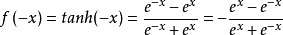
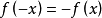
 雙曲正切函式的圖像
雙曲正切函式的圖像


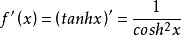

 雙曲正切函式的圖像
雙曲正切函式的圖像



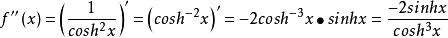
雙曲正切函式(hyperbolic tangent function)是雙曲函式的一種。雙曲正切函式在數學語言上一般寫作tanh,也可簡寫成th。與三角函式一樣,雙曲函式也分為雙曲正弦、雙...
在數學中,雙曲函式是一類與常見的三角函式(也叫圓函式)類似的函式。最基本的雙曲函式是雙曲正弦函式sinh和雙曲餘弦函式cosh,從它們可以導出雙曲正切函式tanh等,...
tanh是雙曲函式中的一個,tanh()為雙曲正切。在數學中,雙曲正切“tanh”是由雙曲正弦和雙曲餘弦這兩種基本雙曲函式推導而來。...
斐波那契雙曲函式(Fibonoacci hyperbolic functions)是一個與黃金分割有關的特殊函式。...
而Sigmoid函式又分為Log-Sigmoid函式(一般所說的S型函式就是這個的簡稱)和Tan-Sigmoid函式(又稱為雙曲正切S型函式),前者的值域為(0,1),後者的值域為(-1,1)...
1 簡介 2 萬能公式的證明 ▪ 幾何證明 3 雙曲函式 正切半角公式簡介 編輯 正切半角公式,又稱萬能公式,這一組公式有四個功能:將...
反雙曲正切函式: 參考資料 1. 胡永忠, 曾平華. 幾個基本初等函式的公理化定義[J]. 廣東教育學院學報, 2001, 21(2): 29-31. 2. 東皋, 小玲. 數學分析...
在神經網路中,隱層和輸出層節點的輸入和輸出之間具有函式關係,這個函式稱為激勵函式。常見的激勵函式有:線性激勵函式、閾值或階躍激勵函式、S形激勵函式、雙曲正切...
本文嘗試利用雙曲正切函式研究單峰、多峰沉積;結果表明雙曲正切函式是識別、估計顆粒分布眾值的一種有效工具,有利於分析控制沉積的地質作用。數學分析法也有利於沉積...
1.37 tan、tanl函式:正切函式1.38 tanh、tanhl函式:雙曲正切函式第2章 字元串函式2.1 atof函式:把字元串轉換成浮點數2.2 atoi函式:將字元串轉換成整型數...
在數學中,雙曲函式是一類與常見的三角函式(也叫圓函式)類似的函式。最基本的雙曲函式是雙曲正弦函式 sinh 和雙曲餘弦函式 cosh,從它們可以導出雙曲正切函式 ...
雙曲函式中的一個,coth()為雙曲餘切。在數學中,雙曲餘切是由基礎雙曲函式雙曲正弦和雙曲餘弦,推導而來。雙曲餘切函式是雙曲正切函式的倒數。...
