基本介紹
- 中文名:內接四邊形
- 外文名:Cyclic quadrilateral
- 分類:數學
- 特點:四個頂點均在圓上
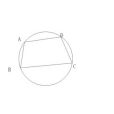
圓內接四邊形(inscribed quadrilateral)是具有四條邊的圓內接多邊形。圓內接四邊形或為凸四邊形或為折四邊形,若為前者,其對角互補;任一外角等於其內對角,如圖2。若為後者,其對角相等。上述兩者其逆命題均成立,它們均是證明四點共...
內接四邊形對角互補(Inscribed quadrilateral diagonal supplementary)是指圓的內接四邊形的對角互補,特點是任意一個外角等於它的內對角,並且四個點都在圓上。定義概述 內接四邊形對角互補:圓的內接四邊形的對角互補,並且任意一個外角等於...
圓內接四邊形 定義 四邊形的四個頂點均在同一個圓上的四邊形叫做圓內接四邊形。性質 (1)圓內接四邊形的對角互補。(2)圓內接四邊形的任意一個外角等於它的內對角。(3)圓的內接凸四邊形兩對對邊乘積的和等於兩條對角線的乘積...
tetragon,英語單詞,主要用作為名詞,用作名詞譯為“ [數] 四角形”。短語搭配 inscribed tetragon 內接四邊形 regular tetragon 正方形 tetragon 2-factor 四邊形2因子 單詞用法 柯林斯英漢雙解大詞典 tetragon /ˈtɛtrəˌɡ...
托勒密(Ptolemy)定理指出,圓的內接凸四邊形兩對對邊乘積的和等於兩條對角線的乘積。 原文:圓的內接四邊形中,兩對角線所包矩形的面積等於 一組對邊所包矩形的面積與另一組對邊所包矩形的面積之和。 從這個定理可以推出正弦、餘弦的和...
若在同一平面內,有四個點在同一個圓上,則稱這四個點共圓,一般簡稱為“四點共圓”。四點共圓有三個性質:(1)共圓的四個點所連成同側共底的兩個三角形的頂角相等;(2)圓內接四邊形的對角互補;(3)圓內接四邊形的外角...
定理圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角 幾何語言:∵四邊形ABCD是⊙O的內接四邊形 ∴∠A+∠C=180°,∠B+∠ADB=180°,∠B=∠ADE 切線的判定和性質 切線的判定定理經過半徑的外端並且垂直於這條半徑的...
是圓內接四邊形,那么對其套用套用托勒密定理就可以得到開世定理:證明完畢。推廣 可以用類似的方法證明,只要當圓 與大圓 相切(不論是外切還是內切),就會有類似開世定理的等式成立。這是需要註明,對任意的i 和j:1、如果圓 是與...
公式無論從形式上還是內容上都是海倫公式的延拓與推廣,但它僅適用於圓內接四邊形。當然, 為四邊形對角和之半時,依然有公式:由於任何n邊的多邊形都可以分割成(n-2)個三角形,所以海倫公式可以用作求多邊形面積的公式,但需要先...
圓內接四邊形對角線的乘積等於兩對邊乘積之和,即托勒密定理在圓中的特殊情況 在四邊形ABCD中,連線AC,作角BAE=角CAD,角ABE=角ACD 則三角形ABE和三角形ACD相似 所以BE/CD=AB/AC,即BE*AC=AB*CD (1)...
65.內接,外接 66.作三角形的內接圓,外接圓法 67.內接四邊形 68.外接四邊形 69.正多角形 70.正多角形的內接圓,外接圓 71.相交的圓 72.相切的圓 73.二圓的位置與中心距離的關係 74.雜例 第四章軌跡及作圖 75.軌跡 76.軌跡的...
圓周上有四點,過其中任三點作三角形,這四個三角形的九點圓圓心都在同一圓周上,我們把過這四個九點圓圓心的圓叫做圓內接四邊形的九點圓。庫立奇-大上定理定理證明 編輯 播報 圖1 如圖1所示,四邊形ABCD是圓內接四邊形,O1,O2,...
∴△ADP∽△CBP (如果一個三角形的兩個角與另一個三角形的兩個角對應相等,那么這兩個三角形相似。)∴AP:CP=DP:BP 即AP·BP=CP·DP 證明二 既然圓內接四邊形定理可以從割線定理而得,那么或許割線定理就可以從圓內接四邊形...
又連線AB,交圓錐曲線於另一點I,連線CI(圖中未畫出),得到圓錐曲線的內接四邊形AICD。設兩組對邊分別交於B、J(J可以是無窮遠點,即AD∥CI),對角線交於K,根據圓錐曲線內接四邊形的調和性質可知JK是B的極線,得到JEKA'共線...
歐氏平面幾何中,婆羅摩笈多公式是用以計算四邊形的面積。它最常用於計算圓內接四邊形面積。基本形式 婆羅摩笈多公式的最簡單易記的形式,是圓內接四邊形面積計算。若圓內接四邊形的四邊長為a, b, c, d,則其面積為:其中s為半...
定理推論 1.在同圓或等圓中,同弧或等弧所對的圓周角相等,相等的圓周角所對的弧也相等。2.半圓(直徑)所對的圓周角是直角;90°的圓周角所對的弦是直徑。3.圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角。
第1節 嵌入三角形的平行四邊形問題 第2節 關於三角形外心的幾個充要條件 第3節 四邊形的中位線的性質及套用 第14章 1992~1993年度試題的詮釋 第1節 圓內接四邊形四頂點組成的四個三角形問題 第2節 圓內接四邊形的兩個充要...
同圓或等圓中,同弧或等弧所對的圓周角相等,相等圓周角所對的弧也相等 半圓(或直徑)所對圓周角是直角,90°的圓周角所對的弦是直徑 圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角。
第5節 四邊形中蝴蝶定理的一些問題(推廣與演變)第12章 1990~1991年度試題的詮釋 第1節 卜拉美古塔定理的推廣及套用 第2節 對角線互相垂直的圓內接四邊形問題 第3節 三角形重心的性質及套用 附錄 1959~1985年IMO中的幾何試題及...
該定理的證明很簡單,利用“圓內接四邊形對角和為180度”及其逆定理。現在已知U是 和 的公共點。連線UM和UN,則四邊形BNUW和四邊形CMUW分別是 和 的內接四邊形,∠UWB+∠UNB=∠UNB+∠UNA=180度,從而∠UWB=∠UNA。同理∠UWB+...
題型19 圓內接四邊形的性質[低頻]題型20切線的判定與性質[高頻]“新”題視角一學科融合 題型21 三角形的外接圓與內切圓[中頻]題型22 正多邊形和圓[中頻]“新”題視角一真實情境 題型23 圓的相關計算[高頻]“新”題視角一真實情境 ...
圓周角等於它所對的弧上的圓心角的一半。③同圓或等圓中,同弧或等弧所對的圓周角相等,相等圓周角所對的弧也相等。④半圓(或直徑)所對圓周角是直角。⑤圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角。
在圓內接四邊形中,兩對角線之積等於兩對對邊之積的和(參看問題研究6.9).研究成果 第二卷是研究與地球的球面性有關的現像。第三、四、五卷,用本輪解釋天文學的地心學說。第四卷中有測量學的三點問題(three—point problem):...
他另一貢獻是托勒密定理,他發現圓內接四邊形兩對對邊乘積的和等於兩條對角線的乘積。定理表述:圓的內接四邊形中,兩對角線所包矩形的面積等於 一組對邊所包矩形的面積與另一組對邊所包矩形的面積之和。從這個定理可以推出正弦、餘弦...
(此處p為凸四邊形的半周),後一結論亦稱“婆羅摩笈多定理”。婆羅摩笈多定理(Brahmagupta theorem):公元七世紀印度數學家婆羅摩笈多曾經證明了下面兩個定理:(1)如果圓內接四邊形的兩條對角線互相垂直,那么過其交點所作一邊的垂線...
則由三角形外角公式:∠P=∠BAD-∠D=1/2(弧BD的度數-弧AC的度數)適用範圍 狹義適用於有關圓內接四邊形的題目,廣義適用於數學領域 具體套用參見1989年捷克斯洛伐克奧林匹克題,現收錄於《國中數學競賽中的幾何問題》一書第十四章B組...
註:其逆定理可作為證明四邊形是圓的內接四邊形的方法. P點若選在圓內任意一點更具一般性。其逆定理也可用於證明四點共圓。比較 相交弦定理、切割線定理及割線定理(切割線定理推論)以及他們的推論統稱為圓冪定理。一般用於求線段長度...
所以△DMN是等腰直角三角形,所以∠DMF=45°,又∠DAF=45°,所以∠DMF=∠DAF,所以四邊形MAFD是圓內接四邊形,所以∠MFD=∠MAD=90°,即DF⊥MN,又DE⊥MN,由此可見,DF和DE是同一條直線,點F和點E實際是同一個點(經過直線外一點有...
