圓內接折四邊形

圓內接折四邊形(inscribed broken quadrilateral in a circle)是與圓相關的一個折四邊形，折四邊形是指有一組對邊相交的複雜四邊形，圓內接折四邊形就是指四個頂點在同一圓上的折四邊形。

基本介紹

• 中文名：圓內接折四邊形
• 外文名：inscribed broken quadrilateral in a circle
• 所屬學科：數學
• 所屬問題：平面幾何（圓，四邊形）
• 簡介：與圓相關的一個折四邊形

基本介紹

圓內接折四邊形是與圓相關的一個折四邊形，指四個頂點在同一圓上的折四邊形。此圓稱為折四邊形的外接圓。

圓內接折四邊形判定定理：如果折四邊形的一組對角相等，那么這個折四邊形內接於圓。

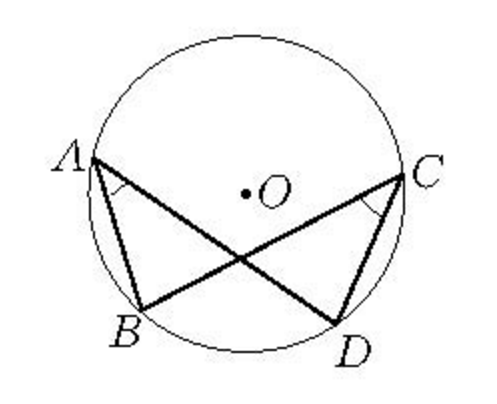
如圖1，折四邊形ABCD中，一組對角∠A=∠C，那么折四邊形內接於一個圓。

反之，圓內接折四邊形性質定理：圓內接折四邊形的兩組對角都相等。

如圖1，折四邊形ABCD內接於⊙O，那么∠A=∠C，∠B=∠D。

圖1 圓內接折四邊形

圓內接四邊形

圓內接四邊形(inscribed quadrilateral)是具有四條邊的圓內接多邊形。圓內接四邊形或為凸四邊形或為折四邊形，若為前者，其對角互補；任一外角等於其內對角，如圖2。若為後者，其對角相等。上述兩者其逆命題均成立，它們均是證明四點共圓的主要定理。

圓內接四邊形相關結論

命題1 設⊙O的圓心，半徑分別為O、R。ABCDE是⊙O的任一內折四邊形(C是折點)。記△CAB、△CDE分別是△₁、△₂。再記： 分別是△_i的內心、內切圓半徑，且 ，則

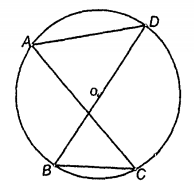
圖4 圓內接折四邊形

命題2 設⊙O的圓心、半徑分別為O、R。ABCD是⊙O的任一內接四邊形。若記△ABC、△ABD分別為△₁、△₂。再記 分別是△_i的內心、內切圓半徑，且，則有

引用察柏爾(chapple)定理，可以獲得下面結論。

命題3記的外心、內心、外接圓半徑、內切圓半徑分別為，且，則有

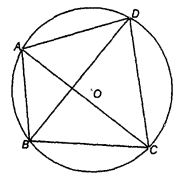
圖5 圓內接折四邊形

察柏爾定理：若△ABC的外接圓半徑、內切圓半徑分別為R、r，而△ABC的內、外心距為d，則R-d=2Rr。

命題4 設⊙O的圓心、半徑分別為O、R。ABCDE是⊙O的任一內折四邊形(C是折點)。記△CAB、△CDE分別是△₁、△₂；再記：分別是的內心、內切圓半徑、外接圓半徑，且，則有

注1 本命題的結果很容易得到：。

注2 若考慮本命題討論圖形的以下極端情況：△CDE退縮為一點，△CAB脹至內接⊙O，則有R-d=2Rr(r、R分別為△ABC的內切圓半徑和外接圓半徑；，是△ABC的內心)。此便是察柏爾定理。

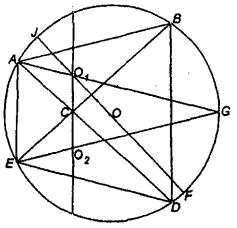
圖6 圓內接折四邊形