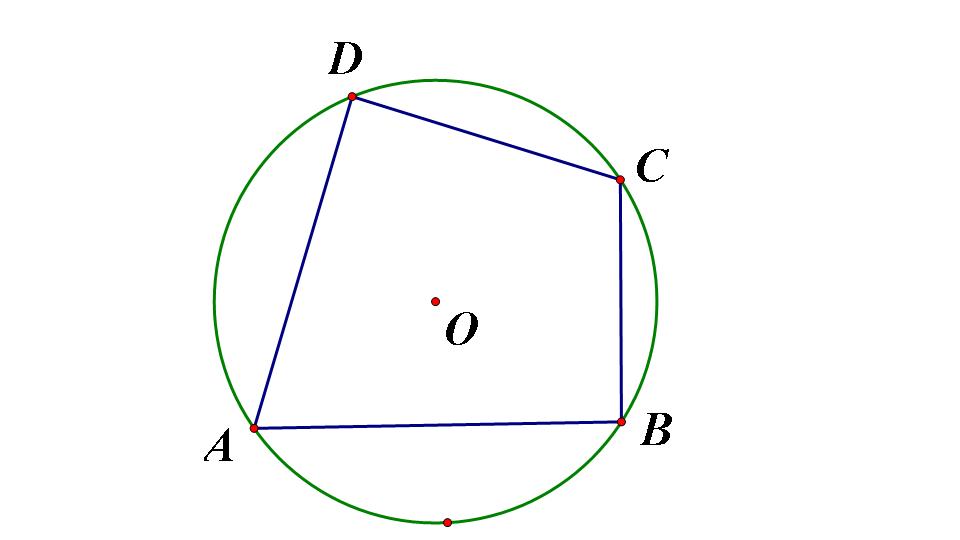
內接四邊形對角互補(Inscribed quadrilateral diagonal supplementary)是指圓的內接四邊形的對角互補,特點是任意一個外角等於它的內對角。
相關詞條
- 內接四邊形對角互補
內接四邊形對角互補(Inscribed quadrilateral diagonal supplementary)是指圓的內接四邊形的對角互補,特點是任意一個外角等於它的內對角。...
- 圓內接四邊形
圓內接四邊形(Cyclic quadrilateral)是一個幾何概念,是指四個頂點均在同一圓上的四邊形。圓內接四邊形擁有很多幾何性質,可用於數學幾何問題求解。...
- 內接四邊形
在同圓內,四邊形的四個頂點均在同一個圓上的四邊形叫做圓內接四邊形,擁有很多有用的性質。圓內接四邊形的面積為√[﹙p-a﹚﹙p-b﹚﹙p-c﹚﹙p-d﹚],[p...
- 內對角
四邊形外角的鄰補角的對角即為此外角的內對角(內對角相對於四邊形外角而言)。...... 圓內接四邊形定理圓內接四邊形:對角互補,外角與內對角相等。共圓的四個點所...
- 圓周角定理
3.圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角。詞條圖冊 更多圖冊 詞條標籤: 科學, 數學, 學科 圖集 圓周角定理圖冊 V百科往期回顧 詞條...
- 四點共圓
四點共圓有三個性質:(1)共圓的四個點所連成同側共底的兩個三角形的頂角相等;(2)圓內接四邊形的對角互補;(3)圓內接四邊形的外角等於內對角。以上性質可以...
- 圓周角度數定理
圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角。詞條標籤: 數學, 學科 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:6次歷史版本 最近更新: ...
- 正弦公式
線段BD是圓的直徑,根據圓內接四邊形對角互補的性質,所以圖4.餘弦公式證明-鈍角時 因為BD為外接圓的直徑 根據正弦定義變形可得根據以上的證明方法可以證明得到得到三角...
- 圓周角定理的推論
⑤圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角。詞條標籤: 數學, 學科 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:8次歷史版本 最近更新:...
- 正弦定理
線段BD是圓的直徑 根據圓內接四邊形對角互補的性質 所以因為BD為外接圓的直徑BD = 2R。根據正弦定義變形可得根據以上的證明方法可以證明得到得到三角形的一條邊與其...
- 四圓定理
推論3如果三角形一邊上的中線等於這邊的一半,那么這個三角形是直角三角形 圓的內接四邊形 定理圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角 幾何語...
- 國中公式
120定理 圓的內接四邊形的對角互補,並且任何一個外角都等於它 的內對角 121①直線L和⊙O相交 d<r ②直線L和⊙O相切 d=r ③直線L和⊙O相離 d>r 122切線...
- 計算公式
120定理 圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角121①直線l和⊙o相交 d﹤r②直線l和⊙o相切 d=r③直線l和⊙o相離 d﹥r122切線的判定...
- 數學公式
120定理 圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角121①直線l和⊙o相交 d﹤r②直線l和⊙o相切 d=r③直線l和⊙o相離 d﹥r122切線的判定...
- 公式(數學術語與其它意義的辭彙)
120定理 圓的內接四邊形的對角互補,並且任何一個外角都等於它 的內對角121①直線L和⊙O相交 d<r②直線L和⊙O相切 d=r③直線L和⊙O相離 d>r122切線的判定...
- 神奇圓周角
圓內接四邊形的對角互補 7.弦切角度數等於所夾弧度數的一半 8.圓內角度數等於此角及其對頂角所對兩弧度數和的一半 9.圓外角度數等於其所夾兩弧度數差的一半[...
- 國中數理化公式定理大全
120定理 圓的內接四邊形的對角互補,並且任何一個外角都等於它 的內對角121①直線L和⊙O相交dr122切線的判定定理 經過半徑的外端並且垂直於這條半徑的直線是圓的...
- 高一數學
120定理 圓的內接四邊形的對角互補,並且任何一個外角都等於它的內對角121①直線l和⊙o相交 d<r②直線l和⊙o相切 d=r③直線l和⊙o相離 d>r122切線的判定...