基本介紹
- 中文名:集合布爾代數
- 外文名:Boolean algebra of sets
- 所屬學科:數學(布爾代數)
- 別名:集合布爾格、集合格
- 簡介:以集合為元素的格
基本介紹





























例題解析




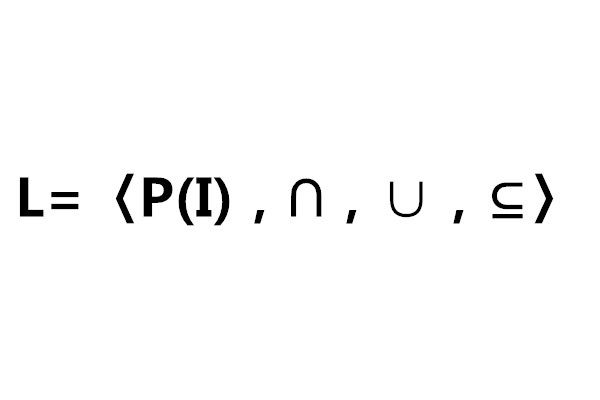

































集合布爾代數(Boolean algebra of sets)亦稱集合布爾格、集合格,是一種特殊的格,指以集合為元素的格,全集I的冪集P(I)對交、並運算是封閉的,對包含於關係“⊆”是偏序的,成為有序集合代數L=〈P(I...
布爾代數B的集合B稱為布爾集,亦稱布爾代數的論域或定義域,它是代數B所研究對象的全體.一般要求布爾集至少有兩個不同的元素0和1,而且其元素對三種運算+,·,′ 都封閉,因此並非任何集合都能成為布爾集.在有限集合的情形,布爾集...
命題的集合P,對命題聯接詞⇁,∨,∧構成的代數結構.就是(P,⇁,∨,∧)。命題代數具有熟知的運算性質,即命題演算(命題邏輯)的基本算律。布爾代數 又稱“邏輯代數”,是英國數學家、邏輯學家布爾(George Boole)1815—1864所...
▪環(ring) ▪布爾代數 基本介紹 播報 編輯 代數系統(algebra system)是建立在集合上的一種運算系統。它是用運算構造數學系統的一種方法,因此稱代數系統。而運算則是一種函式,因此也是一種關係。因此我們說,代數系統是用系統觀點研...
布爾值集全域(universe of Boolean-valuedsets)利用布爾代數對集合全域V的一種擴充.在某個論域上,集合與其特徵函式具有一一對應關係,通常可把它們等同看待.如果把特徵函式的值域擴充為一個布爾代數,那么同一個集合將有多個特徵函式與其...
布爾代數 布爾代數起源於數學領域,是一個用於集合運算和邏輯運算的公式:〈B,∨,∧,¬ 〉。其中B為一個非空集合,∨,∧為定義在B上的兩個二元運算,¬為定義在B上的一個一元運算。通過布爾代數進行集合運算可以獲取到不同...
布爾乘法為集合代數中的交集,亦即表示邏輯積關係,布爾加法為集合代數中的並集,亦即表示邏輯和關係。基本介紹 布爾加法指布爾代數B=〈B,+,·,′,0,1〉中記為+的二元運算,對任意給定的兩個元素a,b∈B,經加法運算後得到一個...
給定集合的子集的代數是完全布爾代數。對應於任何拓撲空間的正規開代數都是完全布爾代數。這個例子特別重要,因為所有力迫偏序集合都可以被認為是一個拓撲空間(給由是小於等於給定元素的所有元素的集合的那些集合組成的拓撲的基)。對應的正規...
在 topos理論中,topos 的子對象分類器接管了真值集合的位置。簡介 定義固定一個完全布爾代數B和一階語言L,後者由一組常量符號、函式符號和關係符號構成。L的布爾值模型因此就由全集M,它是元素(或名字)的集合,和對這些符號的釋義...
下列命題說明對任意集合 S,S的冪集按照包含來排列是個有界格;因此,結合上述的分配律和補集律,它是一個布爾代數。命題 3:若 A,B,C是集合 S 的子集,則下述成立:(1)存在最小元和最大元:(2)存在並運算:若 且 則 。...
兩元素布爾代數是最簡單的布爾代數,它只有兩個元素,習慣指名為 1 和 0。保羅·哈爾莫斯給這個起名為2,被一些文獻和本文採用。任何布爾代數都關聯著叫做“全集”或“載體”的一個偏序集合B,使得這個布爾代數的運算是從Bn到B的映射...
不是生成元的每個B的元素都可被表達為生成元的使用F的元素的有限組合,F是運算的集合;生成元儘可能的獨立,因為對從生成元使用F中運算形成的有限項成立的任何等式,也要對於所有可能的布爾代數的所有元素成立。例子 自由布爾代數的生成...
這個子集滿足對於可數個集合的並集運算和補集運算的封閉性(因此對於交集運算也是封閉的)。σ代數可以用來嚴格地定義所謂的“可測集”,是測度論的基礎概念之一。需要注意的是,雖然σ代數也稱做σ域,但是它是布爾代數。直接定義 設г是...
在數學中,布爾環 R 是對於所有 R 中的 x 有 x²=x 的環,就是說 R 由冪等元素組成。這些環引發自布爾代數。定義 若環R中所有元x都滿足x²=x,則R為布爾環。就是說布爾環 R 由冪等元組成。例子 一個例子是任何集合 ...
設cl(a)表示a的閉包,int(a)表示a的內部,令r(a)=int(cl(a))是a的正則化,如果r(u)=u,則稱u⊆X為正則開集,記RO(X)={u|u⊆X且r(u)=u},RO(X)是關於集合的包含關係構成的完備布爾代數,稱其為X的正則開代數...
B,∨,∧,¬ 〉。其中B為一個非空集合,∨,∧為定義在B上的兩個二元運算,¬為定義在B上的一個一元運算。通過布爾代數進行集合運算可以獲取到不同集合之間的交集、並集或補集,進行邏輯運算可以對不同集合進行與、或、非。
在數學中,剩餘布爾代數是其格結構是布爾代數的剩餘格。介紹 在數學中,剩餘布爾代數是其格結構是布爾代數的剩餘格。例子包括么半群乘法選取為合取的布爾代數,在串接運算之下的給定字母表 Σ 的所有形式語言的集合,在關係複合運算之下...
開關代數(switching algebra)指以開關電路為討論對象的特殊的布爾代數,設K是由一些(抽象的)開關組成的集合,1,0分別表示恆通開關,恆斷開關,∪,∩, - 分別表示開關的並聯,串聯及反相,由此構成的布爾代數〈K,∪,∩, - ,0,1〉稱為...
3.集合環:〈A,∩,∪〉。4.集合域:〈A,∩,∪,〉。5.以全集I的冪集P(I)為基礎集的集合代數:〈P(I),∩,∪,〉,“”表示集合的補運算,這種集合代數是一種布爾代數(參見“冪集代數”)。集合代數與其他代數...
X(集合是閉開的,是指它既是閉集,也是開集).定義介紹 閉開代數(clopen algebra)一種特殊的布爾代數.拓撲空間X的所有閉開子集構成X上的集合代數,稱為X的閉開代數,記為clop X(集合是閉開的,是指它既是閉集,也是開集).
算術布爾代數(arithmetic Boolean algebra)一種特殊的布爾代數.設}'Zl=(A,+,·,‘f O,q M,q )是一個可數布爾代數(即A至多含可數個元素).定義介紹 如果A是自然數集合N的一個算術子集,並且運算+,·和‘是算術的,而且A...
這個定理是斯通氏對偶性的特殊情況,它是在拓撲空間和偏序集合之間的對偶性的一般性框架。在布爾代數的範疇內,態射是布爾同態。在斯通氏空間的範疇內,態射是連續函式。斯通氏對偶性把利用真值表特徵化有限布爾代數推廣到了命題的無限集合。
當可數鏈條件是指與全序集相關的一個概念時,若稠密全序集P中每一個不相交的開區間的集合最多可數,則稱P滿足可數鏈條件,簡記為C.C.C。在布爾代數中,可數鏈條件是指k鏈條件中的k為可數基數時的特殊情況,可數鏈條件簡記為c.c....
命題代數 命題代數(propositional algebra)一種特殊的布爾代數。設W是某一語言中所有命題構成的集合,且設T與F分別為真、假命題,∨,∧,分別為命題的析取,合取,否定聯結詞,則布爾代數〈W,∨,∧,,T,F〉就是命題代數...
並運算 並運算(join)即在格中求兩個元素的上確界的過程。 在布爾代數中,並運算相當於邏輯或運算。在集合論中,並運算相當於並集運算。
這些代數都是布爾代數。關於亨廷頓公理的討論 下面我們討論亨廷頓公理本身的問題。公理是客觀存在的抽象,無需證明。但是可以用客觀存在來驗證。例如我們可以用集合論中的文氏圖來驗證亨廷頓公理。雜亂的公理系統是沒有用處的。 因此, 要想...
