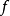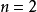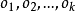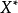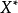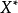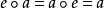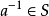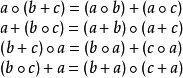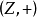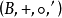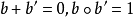基本介紹
代數系統(algebra system)是建立在
集合上的一種運算系統。它是用運算構造數學系統的一種方法,因此稱
代數系統。而
運算則是一種函式,因此也是一種關係。因此我們說,代數系統是用系統觀點研究運算的一種數學,它是關係研究的另一種方法。
代數系統是初等代數和高等代數的一種擴展與抽象的系統。在代數系統中有四個重要概念:運算、系統、運算規則及個體系統。下面對它們進行介紹。
運算
運算是代數系統的基本概念。在初等代數中有
等四則運算,更進一步有
乘方、
開方、
指數、
對數等運算。而將其擴展至
線性代數、高等代數中有向量運算、矩陣運算及行列式運算等。在這裡我們將運算作更為抽象的擴充,使運算不僅包含前面的所有運算,而且還具有更普遍的含義。
我們說:運算是建立在集合S上的n元函式。它可以表示為
。這個
稱為n元運算。當
時稱為一元運算,當
時稱為二元運算,而當
時就稱為多元運算。
這種運算定義具有更廣泛的意義。例如,在計算機中“字元串”的拼接、分解等均為運算;“圖形”中的放大、縮小及旋轉、移位等均屬運算。有了這種擴展性質的運算後,客觀世界(包括計算機世界)中多種“處理手段”都可抽象為運算,從而都可以納入代數系統的討論範圍。因此我們說:運算是對客觀世界對象的一種加工手段與工具。
代數系統
有了運算後就可以建立系統。這種系統稱為代數系統。它由三部分組成:
(3) 運算封閉性——即S中元素經運算後的結果仍在S中。
代數系統的三個條件給出了一個完整系統的基本要素,即加工對象、加工工具和基本約束。這裡所定義的代數系統是一種具有普遍意義的表述,一般常用的是以二元運算為主(一元運算較少見,多元運算基本不用),而在一個系統中一般僅包含一個或兩個運算為多見。
下面給出一些代數系統的例子。
【例1】自然數集N及其“+”運算組成代數系統,即
是代數系統。
【例3】有限個字母組成的集合X,在其上可以構造字母串(稱為句子),它們構成的集合稱為
,對
構造一個並置運算“
”;設
,則
,這樣,
與“
”所構成的
是代數系統。
代數系統用系統的觀點研究數學,將不同集合與運算構成不同的系統以分門別類研究。
運算規則
代數系統是以運算為中心的一種系統。因此,討論代數系統首先要討論運算的規律。運算一般有下面這些主要規律。對
有:
(3)
單位:S中存在唯一一個元素e,對任一
,必有
,e稱為運算
的單位(素)。
(4)
零元:S中存在唯一一個元素0,對任一
,必有
,0稱為運算
的零元(素)。
(5)
逆元:對S中元素
,若存在唯一一個元素
,有
稱為
的逆元(素)。
【例4】整數集及其運算“+”所組成的代數系統
滿足結合律、交換律,並存在單位0,且每個整數必有逆元,如+3之逆元為3;-7之逆元為+7;0的逆元為0等。
著名代數系統
在代數系統中可以按運算的性質不同劃分成為多個個體系統作研究。常用的有:
群(group)
環(ring)
代數系統
如滿足
是群,且滿足交換律,
滿足結合律,
中
對+滿足分配律,則稱為環。
環是代數系統中有兩個二元運算且運算性質不對稱的代表性系統。
布爾代數(boolean algebra)
代數系統
如對+與
都滿足交換律、分配律,有單位與零元,且對一個一元運算“
”有
,則該系統稱為布爾代數。
布爾代數是有兩個二元運算及一個一元運算的典型代數系統。它在計算機中有重要套用。