進程代數是關於通信並發系統的代數理論的統稱。 20世紀70年代後期,英國學者RMnner和C. A.R,分別提出了通信系統演算和通信順序進程,開創了用代數方法研究通信並發系統的先河。 此後這一研究方向興盛不衰,出現了眾多類似而又 相互區別的演算系統,如ACP(提出者J.A.Ber郎tra 和J.W.K10p),ATp(提出者M.H即n櫻y),Meije(提出者G.Eudol,R.desi~),LOTC6等,統稱為進程代數。
基本介紹
- 中文名:進程代數
- 外文名:Process Algebra
簡介,歷史,定義,方法,Bekič,CCS,CSP,中國的研究者,林惠民,
簡介
計算機科學是個非常年輕的科學,非常多的研究至今可能都不超過50年,很多研究的都可以追溯到20世紀50年代,而那個時候從事計算機事業的大師們很多今天仍健在。所以相對而言,我們對與一些事情的歷史可以更加細緻地但不會過於冗長地進行介紹。通過本文,我希望讀者了解到進程代數是什麼,並可以在腦中形成一條簡單的時間線,清楚地看到進程代數發生的歷史。
這些代數理論都使用通信,而不是共享存儲,作為進程之間相互作用的基本手段,表現出面向分散式系統的特徵。 在語法上,進程代數用一組運算元作為進程的構件。運算元的語義通常用結構化操作語義方法定義, 這樣進程就可看成是帶標號的變遷系統。進程代數 的一個顯著特徵是把並發性歸結為非確定性,將並 發執行的進程的行為看成是各單個進程的行為的所 有可能的交錯合成,即所謂交錯語義。 進程代數研究的核心問題是進程的等價性,即在什麼意義下兩個進程的行為相同?在進程代數領域使用的最為廣泛的等價關係有互模擬、測試等價、 失敗等價(參見通信順序進程)等。對這些語義等價 關係均建立了相應的公理系統。關於公理系統的研 究不僅加深了對語義理論的理解,而且使得有可能 對語義等價關係進行形式推理。 為了將進程代數的理論成果套用於解決實際問題,20世紀80年代後期出現了許多計算機支持工具。用這些工具可對進程的行為進行推理或模擬。
歷史
談到進程代數,很多人會想到Petri-net,在進程代數之前,這個1962年由Petri發明的形式化方法是並行理論的唯一工具,用來研究並行和分散式系統。
1970年的時候,世界上關於計算(computation)的形式化推理方法,基本分為三種:
- 操作語義學(Operational semantics)——通過語言的實現方式定義語言的語義,也就是將語言成分所對應的計算機的操作作為語言成分的語義。因為語言的語義應該是標準的,不應依賴於特定的計算機系統,或一種具體的實現方式,因此,操作語義學使用抽象機和抽象解釋程式來定義語言的語義。
- 指稱語義學(Denotational semantics)——通過執行語言成分所要得到的最終效果來定義該語言成分的語義。指稱語義學方法認為語言成分的含義是語言成分本身固有的,不依賴於具體實現該語言成分的計算機。對同一種語言成分,不同的計算機的執行實現過程可以不同,但所產生的最終效果應該是相同的。這種最終效果被看作是語言成分所指稱的外在物體,稱作語言成分的指稱物。指稱物多為數學對象,如整數、集合、函式等。指稱語義學方法在定義語言的語義時,先確定指稱物,然後給出語言成分到指稱物的語義映射,這種映射必須滿足兩個條件:每個語言成分都對應有指稱;複合成分的指稱只依賴於它的子成分的指稱。論域理論是指稱語義學方法的數學基礎。
- 公理化語義(Axiomatic semantics)——通過使用數學中的公理化方法,用公理系統定義程式設計語言的語義。另外,公理語義學還研究和尋求適用於描述程式語義、便於語義推導的邏輯語言。例如,用時態邏輯定義的語言的公理語義又稱為時態語義。典型的公理語義方法是Hoare公理系統。
定義
進程代數英文為:process algebra,在英文中,這個詞組中的process代表一個system(系統的)behavior(行為);一個系統就是一個能表現出各種行為的事物,在計算機世界,process主要指一個軟體系統的行為;這句話很抽象,說白了就是,一個軟體系統可以表現為一個動作(action),比如轉換一個檔案的格式,也可以發生一個個事件(event),比如格式轉換完畢,另外,一個軟體系統也可以。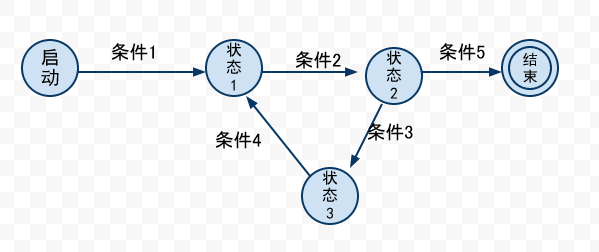

進程代數英文為:process algebra,在英文中,這個詞組中的process代表一個system(系統的)behavior(行為);一個系統就是一個能表現出各種行為的事物,在計算機世界,process主要指一個軟體系統的行為;這句話很抽象,說白了就是,一個軟體系統可以表現為一個動作(action),比如轉換一個檔案的格式,也可以發生一個個事件(event),比如格式轉換完畢,另外,一個軟體系統也可以在一定的序列下完成一系列動作(action);我們可以從各個角度(aspect)去觀察一個系統的行為。研究者往往會關注一個角度的系統行為,這是他們會把系統進行抽象,稱這種抽象為對系統行為的一種觀察(observation)。
有一些研究人員,以這樣的一個角度觀察系統的行為:
系統由一大堆動作(action)組成;
動作之間都是離散的(discrete),獨立的;
離散的意思是action發生在某一時間,各個action發生的時間是獨立的,不相關的。
離散數學中,群(Group)是一個代數結構,它的運算符特性滿足該群的約束要求,比如群(G,*)是一個代數系統,其中運算符*要滿足結合律的要求,從群論的角度來看,進程代數是一個以進程為基本元素,並且進程上的運算符滿足特定的約束的代數結構。
進程代數理論中提出了許多種模型,其中最早的(大約是20世紀中期)、最簡單的模型是:將行為看做是一個帶有輸入/輸出的函式,在進程開始時,給予一個輸入值,在進程的執行過程中的某個時刻會給予外界它的某個輸出值。這個模型是基於有窮自動機理論的,即每個process被看做一個自動機(automaton)【註:今天仍然有人將一個process看作自動機,進行研究】,一個自動機有很多狀態(state)和遷移(transition),狀態通過遷移進行狀態之間之間的轉換,這樣,用自動機代表一個進程時,狀態之間的遷移就代表進程執行了一個動作,所以遷移描述了進程的最基本行為,另外,一個自動機還可以有一個初始狀態和多個終止狀態。一次行為(behiour)就是一個自動機遷移的實例,即從初始態到達某一個終止態的具體路徑過程。
但是後來,人們發現這種自動機模型並不能完全表達一個系統的行為,它無法描述兩個系統之前的互動行為,也就是說自動機無法用來描述並行系統或分散式系統,或者說反應系統(reactive system)的行為。因此人們開始了並發理論(concurrency theory)研究,所以說並發理論是針對反應式、並行式或分散式系統的,這些系統與雲計算也有重要的相關之處。
那么進程代數可以說是並行理論中的一個研究方向,所以我們在後面會看到,一種進程代數通常都會有一個基本的運算符——並行組合(parallel composition),這裡組合(compostion)是指多個離散的動作的組合。除了並行的組合,還有帶有選擇分支的組合(alternative composition--choice)和按順序組合(sequential composition--sequencing),這樣,我們就可以對系統使用進程代數建模,然後通過代數的運算,方程推導進行分析和驗證以判斷系統是否滿足我們所希望的特性。
我們使用加號“ +” 作為 alternative composition, 分號“;” 作為sequential composition,而雙豎線“||” 表示 parallel composition.那么我們定義以下法則:
- – x + y = y + x (commutativity of alternative composition)
- – x + (y + z) = (x + y) + z (associativity of alternative composition)
- – x + x = x (idempotency of alternative composition)
- – (x + y); z = x; z + y; z (right distributivity of + over ;)
- – (x; y); z = x; (y; z) (associativity of sequential composition)
- – x k y = y k x (commutativity of parallel composition)
- – (x k y) k z = x k (y k z) (associativity of parallel composition)
如果任何帶有三個運算符的代數結構滿足以上七條法則,那么就稱這個代數為進程代數,這就是一個簡單的進程代數的概念定義。
方法
Bekič
奧地利維也納的IBM實驗室在整個60年代和70年代都以其程式語言的定義和語義方面的研究而著稱,這個期間Hans Bekič就工作在這裡,他主要從事ALGOL和PL/I(相信學過計算機的同志對這些名詞都有點眼熟)的指稱語義方面的研究,但是針對PL/I的parallel composition運算符如何指定指稱語義遇到了困難,他提出了一個類並行組合運算符(quasi-parallel composition operator),後來更正為並行組合運算符,並提出了一些其他的基本運算和概念,使得進程代數的一些基本概念開始浮現,但是還不成熟。
CCS
進程代數歷史上最重要的人物是Robin Milner,1973至1980年間發明了CCS(Calculus of Communicating Systems,通信系統演算),是用於描述通信並發系統的代數理論。
假定一個標號集L,其補集Act=L∪L∪{τ}稱為動作集,其中τ是特殊的不可見動作。CCS的進程構造運算元如下: 運算元 直觀意義 0 空進程 a.P 動作前綴(a∈Act) P+Q 非確定選擇 P|Q 並行複合 P\S 限制(S L) P[f) 換標號(f是從L到L的部分函式)此外還允許遞歸運算元。 CCS的語義由結構化操作語義方法給出,下面列出幾條典型的語義規則。P→Q表示進程P可執行動作a而演變為Q。 從關於並行運算元|的規則可以看出,由兩個進程並行複合而成的進程可以做每個分進程所能做的動作(PAR1)和(PAR2),但當兩個分進程同時執行一對互補的動作時,則發生通信,產生τ動作(COM)。這種通信方式稱為握手式通信。CCS的基本思想是用τ和+來模擬|,將並發歸結為非確定性,即所謂交錯語義。這一思想體現在下面的展開律中: CCS採用互模擬作為基本的進程等價關係。強互模擬等價滿足下面的Monoid公理: P+0=P,P+P=P,P+Q=Q+P, (P+Q)+R=P+(Q+R) 對觀察等價(將τ忽略不計)還成立三條,—公理: a.τ.P=a.P, P+τ.P=τ.P, a.(P+τ.Q)+a.Q=a.(P+τ.Q) 上面介紹的CCS稱為基本CCS,或純CCS,進程之間只能通過執行互補動作實現同步,而不能直接進行通信。全CCS引入輸出動作c<-e和輸入動作c->x, c<-e表示沿通道c傳送數據表達式e的值,c->x表示從通道c接收一個值賦給x,此外還有條件表達式if- then-else。用全CCS可以直接描述進程間的通信。
CSP
Tony Hoare是另一位重要的人物。1978年C. A.R.Hoare提出的通信順序進程 CSP,是面向分散式系統的程式設計語言。在該語言中,一個並發系統由若干並行運行的順序進程組成,每個進程不能對其他進程的變數賦值。進程之間只能通過一對通信原語實現協作:Q->x表示從進程Q輸入一個值到變數x中;P<-e表示把表達式e的值傳送給進程P。當P進程執行Q->x,同時Q進程執行P<-e時,發生通信,e的值從Q進程傳送給P進程的變數x。後來出現的實用程式語言OCCAM即以CSP為基礎發展而成。 1984年S.Brooks,C.A.R.Hoare和W.Roscoe提出CSP理論(TCSP)。這是一個代數演算系統,其基本成分是事件(或動作)。進程由事件和一組運算元構造而成。典型的運算元有:→(前綴),|(外部非確定性選擇), (內部非確定性選擇) (交錯並行), (同步並行),\e(事件隱蔽),以及遞歸等。 例:(自動售貨機) VM=coin→(choc→VM|coffee→VM), CUST:coin→(choc→CUST coffee→CUST) 這裡定義了兩個進程:VM(售貨機)和CUST (顧客)。售貨機在接受了硬幣coin後,可按顧客的要求支付choc或coffee。顧客在付了硬幣後,或者想要choc,或者想要coffee,其選擇不受外界影響。 與CCS不同(也與作為程式設計語言的CSP不同),TCSP採用的是廣播式通信,而不是握手式通信,即只有當並行運行的各進程都執行同一動作時,才發生同步。 TCSP採用失敗等價作為確定進程等價的準則,這也稱為失敗語義。一個失敗是一二元組(s,X),其中s是事件的有限序列,X是事件集(稱為拒絕集)。若進程P可以執行事件序列s,且到達一個無法執行X中任一事件的狀態,則稱(s,X)是P的一個失敗。例如,設有進程P=a→(b→c→STOP|b→d→STOP),則(ab,{c})是P的一個失敗,因為P可執行ab,變成d→STOP而無法做c。類似地,(ab, {d})也是P的一個失敗,但(ab,{c})不是。兩個進程失敗等價若且唯若它們具有相同的失敗集。例如對自動售貨機的例子,可以證明進程VM|CUST與CUST失敗等價。 利用失敗可以構造TCSP的指稱模型,在此模型中,失敗等價的進程被解釋為同一個元素。關於失敗等價建立了一些公理系統,可以對語義上的等價關係進行形式推導。
中國的研究者
林惠民
林惠民院士主要從事軟體的基礎性研究。計算機是一種工具,大部分的人是在進行套用研究,即如何利用現有的理論和模型來開發出更有用的東西。而基礎性研究與套用研究不同,它不僅要關心怎么樣,還要知道為什麼這樣,要能夠提出新的模型和方法。計算機軟體科學的特點是基礎研究和套用研究是緊密結合的,而且時效性非常強,基礎研究的最新成果很快就會套用到工程中去。林惠民院士從事的一項工作是關於並發程式的形式語義學及形式化方法的研究。他和他的同事設計並實現了世界上第一個通用的進程代數驗證工具。進程代數的實際套用離不開計算機輔助工具的支持。八十年代後期,一批進程代數驗證工具應運而生(如CWB, PSF, LOTOSphere等),其共同局限性是每一工具只適用於某一特定的進程演算。這種局限性妨礙了驗證工具的推廣套用。如何克服這種局限性是當時國際進程代數界面臨的一個重大挑戰。這些驗證工具無法做到通用,根本原因在於缺乏既能描述不同進程演算的語義,又能為計算機所理解的通用語言。經過對不同演算的反覆比較,並考慮到在計算機上實現的可能性,他提煉出了一個元語言,用它可以描述各種進程演算的公理化語義,並且具有良好的可讀性。在此基礎上實現了通用的互動式進程代數驗證工具PAM,只要將這個元語言描述的進程演算定義輸入PAM,就得到該演算的證明器。PAM可同時接受多個不同的演算,對每個演算又可生成多個證明視窗。這是世界上第一個通用的進程代數證明工具。1993年他又利用當時剛剛取得的關於訊息傳送進程證明系統的理論結果,對PAM加以擴充,研製成迄今世界上唯一能對付訊息傳送進程的驗證工具VPAM。PAM和VPAM都是通過ftp在Internet上公開發行的,其用戶遍布各大洲,包括美國、加拿大、英、法、德、意、荷蘭、丹麥、瑞典、斯洛伐克、巴西、印度、紐西蘭、南非等十幾個國家,其中既有來自大學的,也有來自菲利普、惠普和貝爾等著名公司實驗室的。