基本介紹
定義
簡介
代數定義


代數




















範疇論








比較定義



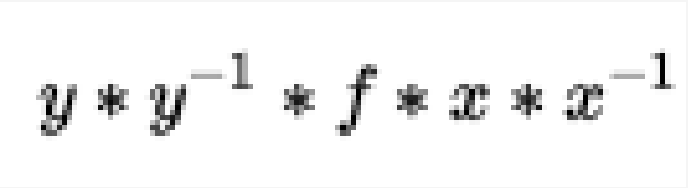
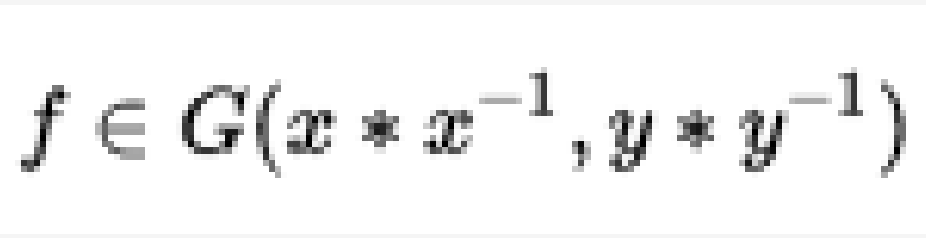




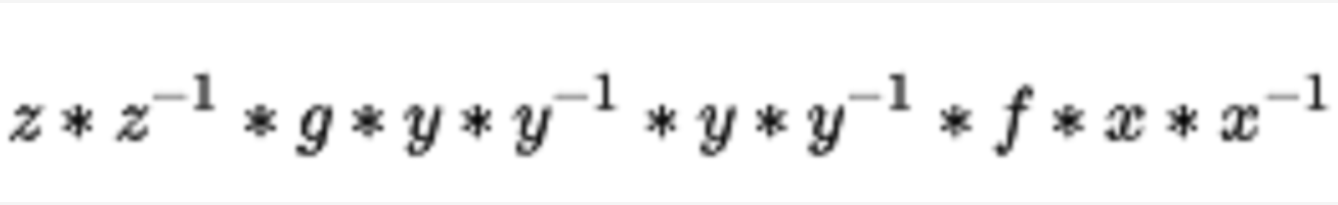



頂點組
舉例
線性代數
拓撲





等價關係



































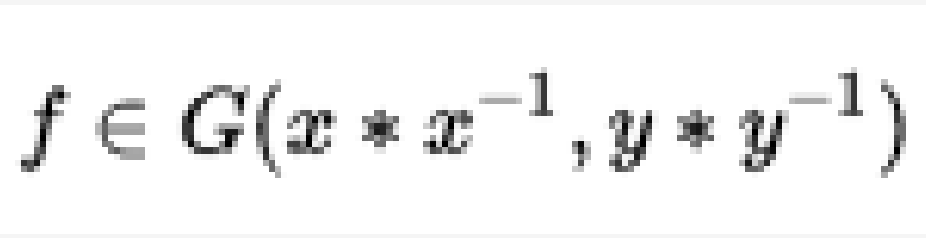




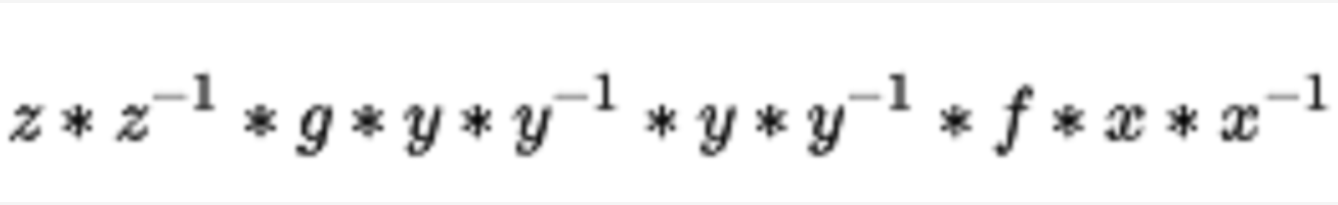









上海廣群網際網路金融信息服務有限公司(即“廣群金融”)成立於2014年11月20日,總部設在上海,通過不斷的技術創新與金融產品設計,提供各種優質的綜合性金融信息服務。公司耗巨資投資金融領域,整合各種資源,積極爭取第三方支付、私募、...
廣群金融是上海廣群網際網路金融信息服務有限公司旗下網站,於2015年2月上線。基本內容 目前累計用戶近30萬,致力於搭建一個高效、透明、安全的智慧型化網際網路理財產品交易平台。廣群金融基於全球金融發展與網際網路技術創新,在健全的風險管控...
張廣群 張廣群,黑龍江省牡丹江市消防救援支隊支隊長。人物履歷 現任黑龍江省牡丹江市消防救援支隊支隊長。
覃廣群,廣西大化人,1995年12加入中國共產黨,1990年7月參加工作,上海交通大學機制專業畢業,工程師。覃廣群,男,壯族,1967年6月生,現任融水苗族自治縣副縣長。1990.07—2002.09柳州佳力電機公司技術員、分公司經理總經理助理 2002....
沙廣群 沙廣群,男,1974年4月生,江蘇邳州人,大學學歷,1992年8月參加工作。現任邳州市人民醫院主任技師,擬任邳州市衛生健康委員會副主任。職務任免 2020年12月,擬任邳州市衛生健康委員會副主任,試用期一年。
喵喵客是上海廣群網際網路金融信息服務有限公司旗下獨立品牌,專注於為廣大投資人搭建一個高效、透明、安全、高回報的網際網路理財產品交易平台。通過與國內頂級銀行、信託、基金、小貸、擔保等專業的金融機構合作,依託強大的風控以及研發團隊,...
在其中可表述(公理化)所有的數學結構(就象傳統上使用集合論可以表示所有數學結構)。一個拓撲斯也可以用來表述一個邏輯理論。4.一個廣群是這樣一種範疇,其中每一個態射都是一個同構。廣群是群、群作用和等價關係的推廣。
上海海貝銀岸信息技術有限公司於2013年02月26日成立。法定代表人劉廣群,公司經營範圍包括:信息技術,計算機科技,網路科技領域內的技術服務、技術諮詢、技術轉讓、技術開發,市場行銷策劃,計算機網路系統工程服務,計算機系統集成,自動售貨...
北方三協半導體(天津)有限公司於2008年06月06日成立。法定代表人薛廣群,公司經營範圍包括:半導體及配件銷售;半導體技術開發、諮詢、服務、轉讓;光電技術開發、轉讓、諮詢、服務;電子產品、機械電子設備(小轎車除外)、儀器儀表、化工...
若G為緊群,則還需要附加條件μ(G)=1。性質 任意局部緊群均有左哈爾測度。設G為局部緊群,μ,ν為G的左哈爾測度。存在c>0,使得μ=cν。對G的任意非空開集U,μ(U)>0。若G為緊群,則μ(G)<∞。廣群的哈爾測度 局部...
槐花村位於吉首市排綢鄉中部,該村東鄰瀘溪縣, 南依香花村,西靠樟武村,北至廣群村。村莊總面積379.86公頃,耕地面積1321.65畝,旱土146畝,林地4095畝,水面65.4畝。槐花村村轄3個村民小組,127戶,619人,其中2013年外出務...
《當代中國政府職能轉變研究》是2008年北京師範大學發表的一篇博士論文,作者是張廣群。副題名 外文題名 論文作者 張廣群著 導師 王章維指導 學科專業 行政管理學 學位級別 博士論文 學位授予單位 北京師範大學 學位授予時間 2008 關鍵字 ...
《Android應用程式開發(第2版)》是2021年2月機械工業出版社出版的圖書,作者是汪杭軍,張廣群,呂鋒華。本書從實用的角度出發,介紹了開發Android套用需具備的基礎知識。內容簡介 《Android應用程式開發(第2版)》是浙江省普通高校“...
雲鶴小區位於武漢市礄口宗關,由武漢住廣群房地產開發有限公司建成,總建築面積100000,總占地面積45000,總計房屋4451戶,小區物業公司為無物業管理服務。周邊配套 醫療 宏愛醫院,普愛醫院(解放大道分院),益豐大藥房(武漢長豐大道雲鶴園...
