亨廷頓公理系統(Huntington axiomatic system)通常用來定義布爾代數〈B,+,·,′,0,1〉的一種公理系統,由亨廷頓(E.V.Huntington)於1904年提出,值得指出的是,這個公理系統中每一條都有兩個式子,它們互為對偶,因此通常把這些條件稱為自對偶的公理系統;然而這個公理系統卻不是獨立的,若將布爾代數的性質3中a+0=a或a·1=a去掉,則由其餘的公理組成的系統才是獨立的。
基本介紹
- 中文名:亨廷頓公理系統
- 外文名:Huntington axiomatic system
- 所屬學科:數學(布爾代數)
- 簡介:用來定義布爾代數的一種公理系統
- 提出者:亨廷頓(E.V.Huntington)
基本介紹,關於亨廷頓公理的討論,
基本介紹
在布爾代數中,有幾種不同的公理系統。但是比較簡單、方便的,乃是美國數學家亨廷頓(Huntington, E. V., 1874--1952)於1904年提出的公理系統:
Ⅰ閉合律:對於全部的x, y∈K,有
(1) (x+y)∈K
(2) (xy)∈K
Ⅱ(1)對於全部的x∈K,存在著元素0∈K,它能使x+0=x
(2)對於全部的x∈K,存在著元素1∈K,它能使x1=x
Ⅲ 交換律: 對於全部的x, y∈K,有
(1) x+y=y+x
(2) xy=yx
Ⅳ分配律:對於全部的x,y, z∈K,有
(1) x+(yz)= (x+y)(x+z)
(2) x(y+z)=x·y+x·z
Ⅴ補:對於每個x∈K,存在著 ,它能使
,它能使

(1)

(2)

Ⅵ至少存在兩個元素x, y∈K,能使x≠y。
把上述公理系統與普通代數中的公理系統加以比較後看出,它們之間有相似之處,也有不同之處。在普通代數中,沒有公理Ⅳ(1)中所示的加對乘的分配律,也沒有補的概念。
這裡著重指出,當K={0,1}時,我們把上述布爾代數叫做二值布爾代數。開關電路中所使用的就是這種二值布爾代數,所以也把它叫做開關代數。此外,因為邏輯命題只有真和假兩種可能,而真和假的值可用1和0代表, 所以有時也把二值布爾代數叫做邏輯代數。這些代數都是布爾代數。
關於亨廷頓公理的討論
下面我們討論亨廷頓公理本身的問題。
公理是客觀存在的抽象,無需證明。但是可以用客觀存在來驗證。例如我們可以用集合論中的文氏圖來驗證亨廷頓公理。
雜亂的公理系統是沒有用處的。 因此, 要想構成一個有用的公理系統,必須滿足三個要求:無矛盾性、獨立性和完備性。下面將分別予以討論。
公理系統內各條公理之間不應當有矛盾。為了證明亨廷頓公理之間無矛盾性,我們可以逐個地研究每條公理,以便推論出每條公理與共他公理不發生矛盾。然而這樣做是非常繁瑣的。為了克服這種繁瑣的證明, 亨廷頓提出了一個巧妙的數學方法。他說如果我們能找到一個布爾代數的例子,並且已知這個布爾代數是沒有矛盾的,那么當這個無矛盾的布爾代數能滿足全部字廷頓公理時,亨廷頓公理系統本身就應當沒有矛盾性。由0和1兩個元素組成的布爾代數,是最簡單的布爾代數,並規定


現在我們把由0和1組成的布爾代數套用於亨廷頓公理系統。我們將看到,根據對這個布爾代數的規定,能滿足各條公理。例如我們先看公理Ⅰ(1)。0,1∈K,則當x=0,y=1時,
0+1=1∈K,
而當x=1,y=0時,
1+0=1∈K,
所以由0和1組成的布爾代數能滿足公理Ⅰ(1)。類似地,也能滿足公理Ⅰ(2)。
再看公理Ⅱ(1)。 如果x= 1,我們有
x+0=1+0=1,
如果x=0,則
x+0=0+0=0,
類似地,也能滿足公理Ⅱ(2)。
再看公理Ⅲ(1)。我們首先列出x,y的值的各種可能組合,並列出各種組合時的x+y和y+x,如圖1所示。這個表叫做公理Ⅲ(1)的真值表。由表中看出,x+y和y+ x這兩列的值是相等的。於是由0和l組成的布爾代數能滿足公理Ⅲ(1)。類似地,也可滿足公理Ⅲ(2)。
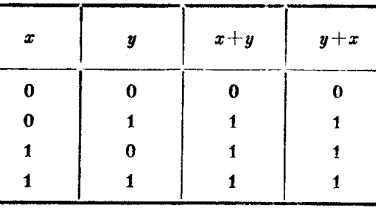
圖1 公理Ⅲ(1)的真值表
用類似的方法,還可證明由0和1組成的布爾代數能滿足其他各條公理。讀者不妨一試。
現在我們討論公理的獨立性。所謂公理的獨立性,是指任何一條公理均不能由另一條公理所證明,也就是說,在公理系統中沒有多餘的公理。上述亨廷頓公理系統是獨立的。證明公理的獨立性這裡不再討論。
這裡需要指出,儘管我們要求公理系統是獨立的,但是非獨立的公理系統無損於公理系統的正確性。事實上,有些作者就採用了非獨立公理系統。這種系統的優點是利用多餘的公理便於推導定理和導出公式。但是採用獨立的公理系統,卻有助於提高讀者運算布爾代數的能力。
所謂公理系統的完備性,是說所有的定理都可以由該公理系統推導出來。稍後,我們將利用公理推導定理。在此之前,我們研兗公理系統中一種有趣的性質,即所謂對偶性。
亨廷頓公理是成對地提出的。我們發現,如果把公理系統中的“+”換成“·”,而把“·”換成“+”,並且把0換成1,而把1換成0,則一對公理中的一個公理可變換成另一個公理。這種性質叫做對偶性。例如圖2
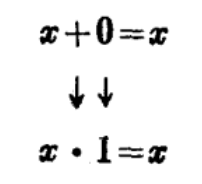
圖2
又如圖3
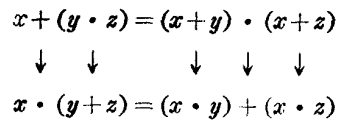
圖3

