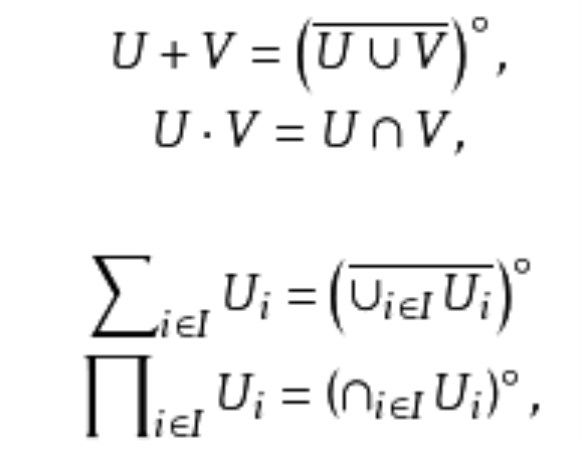正則開代數

正則開代數(regular open algebra)是一種特殊的布爾代數，設X是 一個拓撲空間，對任意a⊆X，設cl(a)表示a的閉包，int(a)表示a的內部，令r(a)=int(cl(a))是a的正則化，如果r(u)=u，則稱u⊆X為正則開集，記RO(X)={u|u⊆X且r(u)=u}，RO(X)是關於集合的包含關係構成的完備布爾代數，稱其為X的正則開代數。

基本介紹

• 中文名：正則開代數
• 外文名：regular open algebra
• 所屬學科：數學
• 所屬問題：布爾代數
• 簡介：一種特殊的布爾代數

相關概念

正則開代數的概念來源於拓撲，要利用拓撲學中的知識討論正則開代數，首先必須定義相關的概念。

設T為集族，若∀U，V∈T(U∪V∈T)，∀S⊆T(∪S∈T)，則稱T為一拓撲。若U∈T，則稱U為開集。令X=U{x |x∈T}，則X∈T，並且∀U∈T(U⊆X)，則稱<X，T>為拓撲空間。若A⊆X ∧(X-A)∈T，則稱A為閉集。若A⊆X，則所有包含A的閉集之交 稱為A的閉包。若U⊆X，x∈X，都存在V∈T使得x∈V∧V⊆U，則稱U為x的鄰域。若A⊆X，x∈A，A是x的鄰域，則稱x為A的內點，A的內點集構成A的內部A°。若U⊆X，若U=( )°，則稱U為正則開集。

設X為拓撲空間，令

Ro(X)={U|U⊆X∧U=( )°}

Ro(x)上的偏序關係為⊆，0，1分別為∅，X，設U，V∈Ro(X)，令

若 ⊆R₀(x)，則

則可以驗證 為一完全布爾代數，稱它為正則開代數(Regular open algebra)。

相關概念及性質

在討論正則開代數的性質時，需幾個相關概念．由於布爾代數是一偏序集，為使概念更具一般性，我們在偏序集上給出這些概念．

設(P，≤)為偏序集，若p，q∈P，都存在r∈P使得r≤P，r≤q，則稱p，q是相容的，否則稱它們是不相容的。若W⊆P，稱D為不相容的，若它的元素之間是兩兩不相容的。若D⊆P，稱D為在P中稠密，若對每一個p∈P，都存在q∈D使得q≤p，若D⊆P，稱D為在p以下稠密，若對每一個p'≤p，都存在q∈D使得q≤p'。若D⊆P，稱D為開的，若p∈D且q≤P，則q∈D。若C⊆P，稱C為P的復蓋，若對每一個p∈P，存在q∈C使得p，q相容。若W⊆P，稱W為D的劃分，若W是D的復蓋且W是不相容的。

再陳述布爾代數的幾個概念。布爾代數B的子代數A稱為在B中稠密，若對B的每一個非o元u，都存在v∈A使得v≤u。

布爾代數B的完備(completion)是一完全布爾代數C，使得B是C的稠密子代數。

若B為布爾代數，P⊆B-{0}，P在B-{0}中稠密，則稱P在B中稠密。

設P是偏序集，若對任意p，q∈P，pq，都存在r≤p使得r與q不可比較，則稱p是可分的。

引理1 設<P，<>是一可分偏序集，則存在唯一完全布爾代數B，使得

[1]P⊆B-{0}，<與B的偏序一致。

[2]P在B中稠密。

引理2 設<P，<>是偏序集，則存在可分偏序集<Q，<>和映射h：P→Q，使得

[1]x≤y→h(x)≼h(y)

[2]x，y∈P，x，y可比較的充要條件為h(x)，h(y)在Q中可比較。

由以上二引理，我們得下列定理。

定理3 設<P，<>為任一偏序集，則存在完全布爾代數B=Ro(P)和映射e：P→B-{0}使得

[1]p≤q→e(p)≤e(q)，

[2]p，q相容↔e(p)·e(q)≠0，

[3]{e(p)|p∈P}在B中稠密，

稱e為P到B內的規範嵌入(Canonical embedding)。

推論4 每一個布爾代數存在唯一的完備。