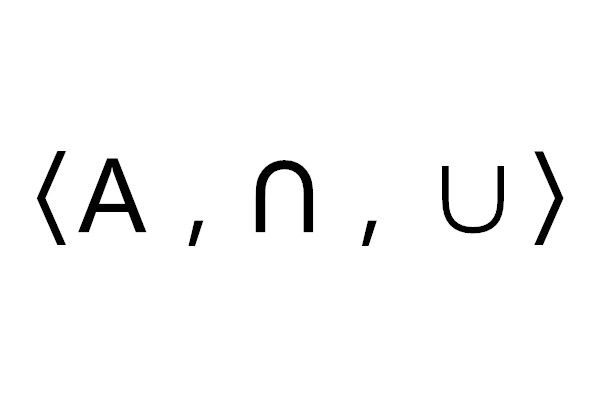集合環(ring of sets)簡稱集環，是一種常見的集合代數。如果由集合構成的非空族R滿足：A∈R和B∈R蘊涵A∪B ∈R，A-B∈R，則稱R為一個集環。如果它還滿足An∈R(n=1,2,…)蘊涵∪n=1An∈R，則稱R為σ(集)環。如果把兩個集合的對稱差看作和，把兩個集合的交看作積，則上面定義的集環就是在這兩種運算下的代數意義上的環。對任何集合X，它的一切有限子集構成的族S是一個集環。左閉右開區間的一切有限並構成一個集環。設C是由集合X的一些子集構成的一個族，則一切包含C的集環(或σ環)的交是包含C的最小集環(或σ環)，稱為由C生成的集環(或σ環)。
基本介紹
- 中文名：集合環
- 外文名：ring of sets
- 簡稱：集環
- 所屬學科：數學（集合論）
- 簡介：集環
基本介紹,集合環的性質,集合代數,
基本介紹
集合E的全體子集之集P(E)的任一非空子集， 如果它對有限並及差的運算是穩定的，則稱它為集合E的集（合）環， 從而集環對於有限交運算亦是穩定的，例如，R上兩兩不相交的有界區間的有限並之全體構成R的集環，更一般地，R上兩兩不相交的有界長方體的有限並之全體構成Rn的集環，包含由集合E的子集所成的已知集合A的所有集環的交還是集環，稱為由A生成的集環。
集合環的性質
集合環是一種常見的集合代數。若A為一非空集族，且對於任意A∈A，B∈A，均有A∩B∈A，A∪B∈A，則稱A在集合的交、並運算下成一集合環，記為〈A，∩，∪〉.其中A稱為集合環的基礎集族，∩與∪是集合環的運算.U=〈A，∩，∪〉是集合環的條件可以用符號表述為∀A∀B(A∈A∧B∈A→A∩B∈A∧A∪B∈A)。
集合環有下列性質：
1.設U=〈A，∩，∪〉，A1，A2，…，An∈A，則：
2.設Ui=〈Ai，∩，∪〉(i=1，2)是集合環，則U1∩U2=〈A1∩A2，∩，∪〉也是集合環。例如，Ui=〈Ai，∩，∪〉(i=1，2)是集合環，當A1
A2時，稱U1是U2的子集環，U2是U1的母集環。
3.對任何集族M，存在一個包含它的最小集合環U=〈A，∩，∪〉，使MA，這隻要取M中有限個元素的有限交的有限並來構成A就行了。
集合代數
集合代數亦稱冪集代數，是一種特殊的集合族的代數。如果集族A的元素對於指定的某些集合運算封閉，這些運算滿足若干公理，就稱集族A關於這些運算在指定公理體系下成為一個集合代數。例如，集合環、集合域等都是集合代數。這裡A稱為這個集合代數的基礎集(族)，這些運算稱為集合代數的運算。
常見的集合代數如下：
1.對於集合的並運算封閉的集族A作成的並代數：〈A，∪〉。
2.對於集合的交運算封閉的集族A作成的交代數：〈A，∩〉。
3.集合環：〈A，∩，∪〉。
4.集合域：〈A，∩，∪，〉。
5.以全集I的冪集P(I)為基礎集的集合代數：〈P(I)，∩，∪，〉，“”表示集合的補運算，這種集合代數是一種布爾代數(參見“冪集代數”)。
集合代數與其他代數不同之點是：
1.它以集族為基礎集合。
2.它的運算是集合運算。
3.它的公理體系就是在集合運算的基本性質上添上或不添上若干附加要求。
