基本介紹
- 中文名：運算元同態
- 外文名：operator homomorphism
- 領域：數學
- 學科：代數
- 定義：一般群的同態
- 地位：同構在運算元群上的推廣
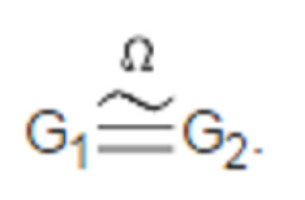
概念,群,運算元群,同態,群的同態,同構,
概念
運算元同態(operator homomorphism)是指一般群的同態，是同構在運算元群上的推廣。設G1，G2為兩個運算元群，Ωi分別為Gi的運算元集 (i=1，2)。若G1與G2同態，Ω1與Ω2之間存在一一映射α1α2(αi∈Ωi，i=1，2)，使得在G1與G2的同態下，即當gi∈Gi(i=1，2)，g1→g2時恆有g1→g2，則稱G1與G2關於Ω1，Ω2是運算元同態的。當上述G1與G2間的同態為同構映射時，稱G1與G2為運算元同姜妹鞏船構，記為：
運算元同態(同構)又稱為Ω同態(同構)，或容許同態(同構)。
群
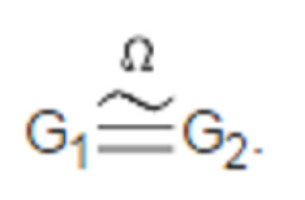
群是一種只有一個運算的、比較簡單的代數結構；是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合，a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”，運算結果稱為“乘積”)滿足：
(1)封閉性，a·b∈G;
(2)結合律，即(a·b)c = a·(b·c);
(3)對G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，則稱G對於所定義的運算“·”構成一個群。例如，所有不等於零的實數，關於通常的乘法構成一個群;時針轉動(關於模12加法)，構成一個群。
滿足交換律的群，稱為交換群。
群是數學最重要的概念之一，已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱，就存在群。例如，可以用研究圖形在變換群下保持不變的性質，來定義各種幾何學，即利用變換群對幾何學進行分類。可以說，不了解群，就不可能理解現代數學。
1770年，拉格朗日在討論代數方程根之間的置換時，首先引入群的概念，而它的名稱，是伽羅華在1830年首先提出的。
運算元群
運算元群亦稱帶算群或稱Ω群。比群更廣且有重要運用價值的群類。群G到G的一個映射α：gg稱為G的一個運算元，若對於任意的x，y∈G，均有(xy)=xy。G的一個運算元就是G的一個自同態。G的某些運算元做成的集合，稱為G的一個算局榜艱盛子集.運算元集常用Ω記。帶有運算元集的群稱為帶算群，或運算元群，或Ω群。設H是群G的子群，Ω是G的一個運算元集，若對任意的α∈Ω，h∈H，均有h∈H，則稱H是G的Ω容許子群(Ω不變子群)。當Ω是G的全懂主道體內自同構所成之集時，G的Ω容許子群就是G的正規子群；當Ω是G的全體自同構所成之集時，恥試G的Ω容許子群就是G的特徵子群。運算元群的理論與一般群的理論是平行的，群的一般理論都可以推廣到運算元群上去，且取定適當的運算元集，有時還可以提高對群本身的研究效果。而一般的群可以看成運算元集為空集的群。
同態
設E與F為兩個群胚，它們的合成法則分別記為⊥與⊤。稱從E到F中的映射f是群胚同態，如果對於E的任一元素偶(x，y)，有：
設E與F為兩個么半群(兩個群)，稱從E到F中的映射。f是么半群(群)的同態，如果f是群胚的同態，且E的中性元素的象是F的中性元素。(在群的情況下，後一個條件是自然滿足的，但是從加法么半群N到乘法么半群N的映射x↦0是群胚的同態， 而並不因此就是么半群的同態)。
設G為乘法群，而a為G的元素。由關係f(n)=an所定義的從乃應棄加法群Z到G中的映射f是群的同態。
設A與B為兩個環(兩個體)，稱從A到B中的映射f是環(體)的同態，如果f是加法群的同態，且為乘法么半群炒拘永的同態。這就是說，對A的任一元素偶(x，y)，有：
f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，
並且f將A的單位元變成B的單位元。
例如，設n為非零自然數；使任一有理整數對應其對模n的剩餘類映射是從環Z到環Z/nZ上的同態。設E與F為兩個A-代數(兩個酉A-代數)。稱從E到F中的映射f是A-代數(酉A-代數)的同態，如果它是線性映射，並且是乘法群胚(乘法么半群)的同態。
例如，設E為交換體K上的非零有限n維向量空間，而B為E的基。 則從E的全體自同態之酉代數ℒ(E)到K中元素膠凝影構成的全體n階方陣之酉代數Mn (K)中的映射，如果該映射使E的任一自同態對應它在基B中的矩陣，則這一映射是酉代數的同態。
同態的概念能用抽象的方式加以推廣。
群的同態
一類重要的映射。群之間的保持運算的一類映射。設f是群G到群G′(不必異於G)的映射，若f保持運算，即對所有的x，y∈G，總有f(xy)=f(x)f(y)(或(xy)=x·y)，則稱f是群G到群G′的同態映射，簡稱同態。若同態映射f還是一個雙射，則稱f為G到G′的同構映射，記為GG′.這時稱群G和G′同構，記為GG′。特別地，若G=G′時，則分別稱f為群G的自同態和自同構。
同構
兩個數學系統(例如兩個代數系統)，當它們的元素及各自所定義的運算一一對應，並且運算結果也保持一一對應，則稱這兩個系統同構，記為≌。它們對於所定義的運算，具有相同的結構。例如，十進制數與二進制數是同構的。
建立同構關係的映射，稱為同構映射。例如，當映射為一一映射，並且對應元素關於運算保持對應時，就是同構映射。
同構是數學中最重要的概念之一。在很多情況，一個難題往往可以化成另一個同構的、似乎與它不相關的、已經解決的問題，從而使原問題方便地得到解決。雖然數學發展得越來越複雜，但利用同構概念，不僅使數學得到簡化，而且使數學變得越來越統一。表面上似乎不同，但本質上等價的結果，可以用統一的形式表達出來。例如，如果四色定理得到了證明，其他數學分支中與它同構的幾十個假設，也同時得到了證明。
同態
設E與F為兩個群胚，它們的合成法則分別記為⊥與⊤。稱從E到F中的映射f是群胚同態，如果對於E的任一元素偶(x，y)，有：
設E與F為兩個么半群(兩個群)，稱從E到F中的映射。f是么半群(群)的同態，如果f是群胚的同態，且E的中性元素的象是F的中性元素。(在群的情況下，後一個條件是自然滿足的，但是從加法么半群N到乘法么半群N的映射x↦0是群胚的同態， 而並不因此就是么半群的同態)。
設G為乘法群，而a為G的元素。由關係f(n)=an所定義的從加法群Z到G中的映射f是群的同態。
設A與B為兩個環(兩個體)，稱從A到B中的映射f是環(體)的同態，如果f是加法群的同態，且為乘法么半群的同態。這就是說，對A的任一元素偶(x，y)，有：
f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，
並且f將A的單位元變成B的單位元。
例如，設n為非零自然數；使任一有理整數對應其對模n的剩餘類映射是從環Z到環Z/nZ上的同態。設E與F為兩個A-代數(兩個酉A-代數)。稱從E到F中的映射f是A-代數(酉A-代數)的同態，如果它是線性映射，並且是乘法群胚(乘法么半群)的同態。
例如，設E為交換體K上的非零有限n維向量空間，而B為E的基。 則從E的全體自同態之酉代數ℒ(E)到K中元素構成的全體n階方陣之酉代數Mn (K)中的映射，如果該映射使E的任一自同態對應它在基B中的矩陣，則這一映射是酉代數的同態。
同態的概念能用抽象的方式加以推廣。
群的同態
一類重要的映射。群之間的保持運算的一類映射。設f是群G到群G′(不必異於G)的映射，若f保持運算，即對所有的x，y∈G，總有f(xy)=f(x)f(y)(或(xy)=x·y)，則稱f是群G到群G′的同態映射，簡稱同態。若同態映射f還是一個雙射，則稱f為G到G′的同構映射，記為GG′.這時稱群G和G′同構，記為GG′。特別地，若G=G′時，則分別稱f為群G的自同態和自同構。
同構
兩個數學系統(例如兩個代數系統)，當它們的元素及各自所定義的運算一一對應，並且運算結果也保持一一對應，則稱這兩個系統同構，記為≌。它們對於所定義的運算，具有相同的結構。例如，十進制數與二進制數是同構的。
建立同構關係的映射，稱為同構映射。例如，當映射為一一映射，並且對應元素關於運算保持對應時，就是同構映射。
同構是數學中最重要的概念之一。在很多情況，一個難題往往可以化成另一個同構的、似乎與它不相關的、已經解決的問題，從而使原問題方便地得到解決。雖然數學發展得越來越複雜，但利用同構概念，不僅使數學得到簡化，而且使數學變得越來越統一。表面上似乎不同，但本質上等價的結果，可以用統一的形式表達出來。例如，如果四色定理得到了證明，其他數學分支中與它同構的幾十個假設，也同時得到了證明。
