基本介紹
- 中文名:常係數微分運算元
- 外文名:differential operator with constant coefficients
- 所屬學科:數學
- 所屬問題:偏微分方程(線性偏微分運算元)
- 相關概念:線性偏微分運算元,偏微分運算元等
基本介紹
基本解的存在性定理








亞橢圓常係數微分運算元


















施瓦茲定理











定強微分運算元










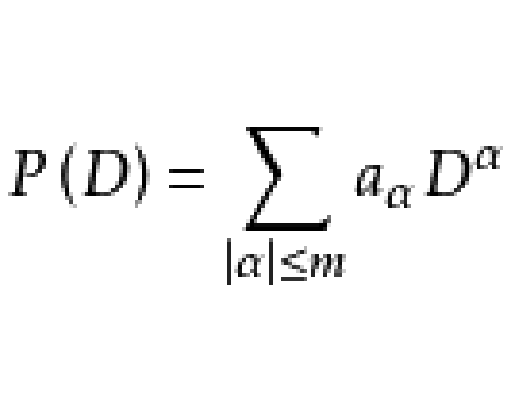















































(1)微分是線性的,即 D(f+g)=(Df)+(Dg)D(af)=a(Df)這裡f和g是函式,而a是一個常數。(2)任何以函式為係數之D的多項式也是一個微分運算元。我們也可以通過法則 (3)複合微分運算元。需要一些注意:首先運算元D₂中的任何...
微分運算元法(method of differential operator)是1993年經全國科學技術名詞審定委員會審定公布的數學名詞。一般形式 階常係數非齊次線性常微分方程的一般形式是 其中 為實常數 運算元多項式 定義 對於函式 規定下列記號及其意義:記 ,稱為...
微分運算元法:微分運算元法是求解不同類型常係數非齊次線性微分方程特解的有效方法,使用微分運算元法求解二階常係數非齊次線性微分方程的特解記憶較為方便,計算難度也可降低。引入微分運算元d/dx=D,d^2/dx^2=D^2,則有 y'=dy/dx=...
第四章和第五章分別給出了半群理論對常係數抽象微分運算元和偏微分運算元的套用,對比了用正則半群和積分半群所得結果,表明了正則半群是處理非橢圓偏微分運算元的適當工具。第六章介紹了正則半群對時變係數非橢圓微分運算元的套用。第七章...
線性微分方程的一般形式是:其中D是微分運算元d/dx(也就是Dy = y',D²y = y",……), 是給定的函式。這個微分方程是n階的,因為方程中含有y的n階導數,而不含n+1階導數。如果ƒ = 0,那么方程便稱為齊次線性微分方程...
一般自伴運算元 很多數學分析中的重要線性運算元,例如微分運算元,是無界的。對於這類情況的自伴運算元也有一個譜定理。例如,任何常係數微分運算元酉等價於乘法運算元。事實上,實現這一等價的酉運算元就是傅立葉變換;該乘法運算元是一類傅立葉乘子。
《樣條函式與再生核》在樣條函式的基礎部分著重介紹了B-樣條和LB-樣條的構造和遞推性;系統地研究了多項式再生核與微分運算元再生核的構造和計算,對一類常係數微分運算元確定的再生核的計算進行了詳細討論;用再生核方法證明了自然L-插值樣條...
其中對多項式代數收縮的刻畫還有助於研究Jacobi猜想和Zariski消去問題. (2)研究多項式代數自同構到自由metabelian代數和自由結合代數的提升問題,構造這些代數上新的tame或wild 自同構類. (3)研究多項式代數上一階常係數微分運算元的像以及局部...
《再生核的理論與套用》的主要特色:將W2m嚴空間的內積和再生核理論納入半內積空間理論的統一框架;用Green函式方法統一討論W2m嚴空間的再生核的構造;對幾類常係數微分運算元所對應的再生核進行了詳細討論,並探討了再生核理論中的GrPen...
先後在《內蒙古大學學報》上發表論文6篇:“Whitham-Broer-Kaup-Like方程的一般形式的精確解(英文稿)”、“Whitham-Broer-Kaup-Like方程的新的行波解(英文稿)”、“常係數J-自伴Eulerwei微分運算元的本質譜”、“常係數J-自伴微分...
局部可解性,是指研究線性偏微分方程Pu=ƒ在什麼條件下局部有解存在。定義 研究線性偏微分方程Pu=ƒ在什麼條件下局部有解存在。若P是常係數運算元,則由基本解的存在而保證Pu=ƒ一定局部有解。在變係數情況下,柯西-柯瓦列夫斯卡婭...
第二章 線性偏微分方程的解法 2.1 一階線性偏微分方程的解法 2.1.1 一階線性方程的求解 2.2 二階線性偏微分方程的通解 2.3 常係數方程通解的行波解 2.4 常係數方程通解的微分運算元法 2.4.1 微分運算元法 2.4.2 簡化的微分...
從1955年起,他先後參與建 立線性偏微分運算元四大理論:線性常係數偏微分方程理論;線性變係數偏微分方程理論( 這個理論與常係數情形大不相同);偽微分運算元理論(它與指標理論密切相關,而指標理 論是拓撲與分析的密切結合,是20世紀數學...
偽微分運算元 主條目:偽微分運算元 偽微分運算元的想法可以用歐氏空間上的常係數偏微分運算元解釋。這些運算元不外是多項式函式的傅立葉變換;如果我們容許更一般的函式,其傅立葉變換就構成了偽微分運算元。對於一般的流形,可以透過局部坐標系定義偽...
赫爾曼德爾的主要研究領域是線性及非線性偏微分方程理論。從1955年起,他參與建立偏微分運算元四大理論:線性常係數偏微分方程理論、線性變係數偏微分方程理論、偽微分運算元理論、傅立葉運算元理論。這些成就總結在四卷本《線性偏微分運算元的分析》...
第10講 Bony的仿微分運算元與仿線性化技術 第11講 新型的Bernstein不等式 第12講 常係數偏微分方程的局部可解性及解的正則性 第13講 數學物理中的基本運算元 第14講 線性Schrodinger方程解的Strichartz估計與光滑效應 第15講 非線性...
是定義在n維歐幾里得空間某個開集Ω上的函式,當n=1時,P(x,D)是常微分運算元;當n≥2時,P(x,D)是偏微分運算元。偏微分方程 未知函式具有多個自變數,含有這種未知函式的一個或多個偏導數的微分方程稱為偏微分方程。如自變數只有一...
