如果一個平面圖形沿著一條直線摺疊後，直線兩旁的部分能夠互相重合，那么這個圖形叫做軸對稱圖形（a figure has reflectional symmetry），這條直線叫做對稱軸（axis of symmetry）。
註：斜放的圖形只要能沿一條直線摺疊，直線兩側的圖形能夠互相重合，就是軸對稱圖形。在軸對稱圖形中間畫一條線，那條線叫對稱軸。
基本介紹
- 中文名：軸對稱
- 外文名：symmetric
- 學科：數學
- 性質：全等、垂直平分線
- 例題：3大類
- 軸對稱圖形：9種
定義,性質,套用,意義,舉例,圖形及對稱軸,
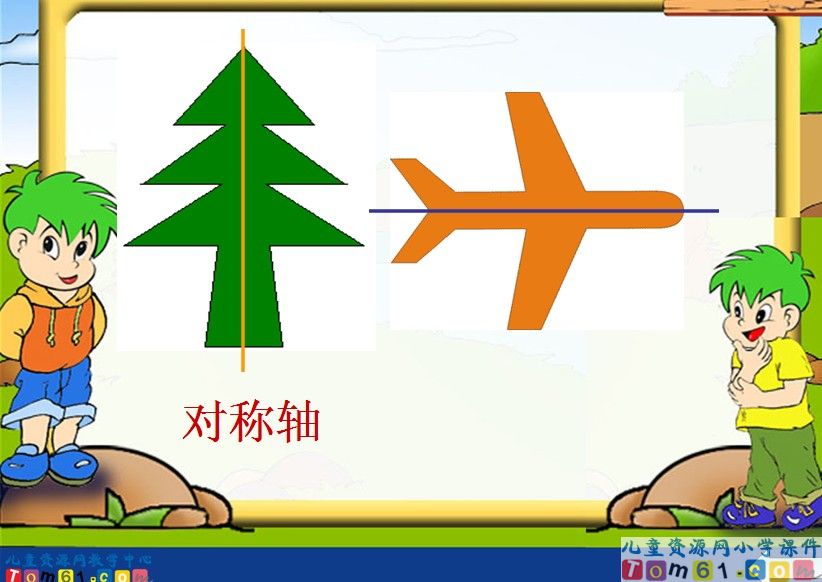
定義
在人教版老教材第十一冊中指出“如果一個圖形沿著一條直線對摺，兩側的圖形能夠完全重合，這個圖形就是軸對稱圖形"。蘇教版中指出：一個圖形如果沿某條直線對摺，對摺後摺痕兩邊的部分是完全重合的，那么就稱這樣的圖形為軸對稱圖形。梳子的圖片也是軸對稱圖形。註：斜放的圖形只要能沿一條直線摺疊，直線兩側的圖形能夠互相重合，就是軸對稱圖形。在軸對稱圖形中間畫一條線，那條線叫對稱軸。
性質
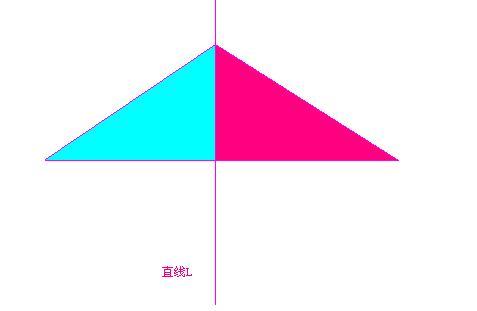
像右圖，把一個圖形沿著某一條直線摺疊，如果它能夠與另一個圖形重合，那么就說這兩個圖形關於這條直線對稱，這條直線叫做對稱軸，摺疊後重合的點是對應點（symmetric points）,叫做對稱點。軸對稱和軸對稱圖形的特性是相同的，對應點到對稱軸的距離都是相等的。
軸對稱
軸對稱軸對稱圖形具有以下的性質：
（1）成軸對稱的兩個圖形全等；
（2）如果兩個圖形成軸對稱，那么對稱軸是對稱點連線的垂直平分線；
經過線段中點並且垂直於這條線段的直線，叫做這條線段的垂直平分線（perpendicular bisector）。這樣就得到了以下性質：
2.類似地，軸對稱圖形的對稱軸，是任何一對對應點所連線段的垂直平分線。
3.線段的垂直平分線上的點與這條線段的兩個端點的距離相等。
4.對稱軸是到線段兩端距離相等的點的集合。
套用
可以通過對稱軸的一邊從而畫出另一邊。
可以通過畫對稱軸得出的兩個圖形全等。
擴展到軸對稱的套用以及函式圖像的意義。
意義
關於平面直角坐標系的X,Y對稱意義
如果在坐標系中，點A與點B關於直線X對稱，那么點A的橫坐標不變，縱坐標為相反數。
相反的,如果有兩點關於直線Y對稱,那么點A的橫坐標為相反數,縱坐標不變。
關於二次函式圖像的對稱軸公式
也叫做軸對稱公式
設二次函式的解析式是y=ax^2+bx+c
則二次函式的對稱軸為直線x=-b/2a,頂點橫坐標為-b/2a,頂點縱坐標為(4ac-b^2)/4a
另外，如果遇到的圖形不是軸對稱圖形，則常選擇某直線為對稱軸，補添為軸對稱圖形，或將軸一側的圖形通過翻折反射到另一側，以實現條件的相對集中．
舉例
例1△ABC中，P為∠A外角平分線上一點，求證：PB+PC>AB+AC．
分析：由於角平分線是角的對稱軸，作AC關於AP的軸對稱圖形AD，連結DP，CP，則DP=CP，BD=AB+AC．這樣，把AB+AC，AC，PB，PC集中到△BDP中，從而由PB+PD>BD，可得PB+PC>AB+AC．
證：（略）．
點評：通過變為軸對稱圖形後，起到相對集中條件的作用，又有將折線化直的作用（如AB+AC化直為BD）．
例2 等腰梯形的對角線互相垂直，且它的中位線等於，求此梯形的高．
解：如圖3．設等腰梯形AD∥BC，AB=DC，對角線AC與BD相交於O，且AC⊥BD，中位線EF=m.過AD，BC的中點M，N作直線，由等腰梯形ABCD關於直線MN成軸對稱圖形，∴O點在MN上，且OA=OD，OB=OC，AM=DM，BN=CN．又AC⊥BD，故△AOD和△BOC均為等腰直角三角形．2OM=AD，2ON=BC．∵AD+BC=2EF=2m，∴2OM+2ON=2m．
∴OM+ON= ，所以梯形高MN=m．
確定點的位置找最小值
例1 AB∥CD，AC⊥CD，在AC上找一點E，使得BE+DE最小。
解：作點B關於AC的對稱點B′，連線DB′，交AC於點E，點E就是要找的點。
例2 如圖4，點A是總郵局，想在公路L1上建一分局D，在公路L2上建一分局E，使AD+DE+EA的和最小．
解：作點A關於L1和L2的對稱點B、C．連線BC，交L1於點D，交L2於點E．點D、E就是要找的點。
例3 要在河岸所在直線l上修一水泵站，分別向河岸同側的A、B兩村送水，請你設計水泵站應修在何處，所用管道最短？分析：設水泵站修在C點，此題的實質是求折線AC+BC的最短長度，可作出A點關於直線l的對稱點A′，如圖1，根據對稱性，AC+BC=A′C+BC，所以連結BA′交直線l於點C，點C便是水泵站的位置，因為此時折線長AC+CB化成線段A′B的長，根據兩點之間線段最短的道理便可確定點C是水泵的位置。
例5
例5與其它學科的結合
唐朝某地建造了一座十佛寺，竣工時，太守在廟門右邊寫了一副上聯“萬瓦千磚百匠造成十佛寺”，望有人對出下聯，且表達恰如其分。
對聯中有數字萬、千、百、十，幾個月過去了，無人能對，有個文人李生路過，感覺廟前沒有下聯不像話，十分感慨。一連幾天在廟前苦思冥想，未能對出下聯，有次在廟前散步，望見一條大船由遠而來，船夫正使勁的搖櫓，這時李生突發靈感，對出了下聯———“一舟二櫓四人搖過八仙橋”。
太守再次路過此廟時，看到下聯，連連稱讚“妙妙妙”．這副對聯數字對數字，事物對事物，對稱美如此的和諧。可見，對稱美在文學方面也有生動深刻的體現。
生活中的軸對稱無處不在，只要你善於觀察，將會發現其間所蘊涵的豐富的文化價值和對稱美給人帶來的回味無窮的享受。
對稱之後解方程
求有關最小值問題，經常利用對稱的思想轉移點的位置，改變思維角度，再利用（直線）一次函式的解析式求得最小值點的坐標，真正體現出“數形結合”的數學思想。
例1 已知兩點A（0，2），B（4，1），點P是x軸上的一點，且PA+PB的值最小，求點P的坐標。
分析：如圖1，在坐標系中先標出點A、B的位置，在x軸上要確定一點P，使PA+PB最小，先作出點A關於x軸的對稱點A′，連結A′B，與x軸交於點P，根據“兩點之間，線段最短”的道理，點P就是要求的點（如果另取一點P′，則P′A+P′B>PA+PB，這些都應該考慮到）．
例2 某公路的同一側有A、B、C三個村莊，要在公路邊建一貨站D，向A、B、C三個村莊送農用物資，路線是D→A→B→C→D或D→C→B→A→D．將A、B、C三點畫在平面直角坐標系中，x軸為公路，貨站要建在公路邊上，且要保證送貨路程最短，請畫出點D的位置，並求出點D的坐標．
分析：假設點D已確定，送貨路程之和為DA+AB+BC+CD，因為點A、B、C的位置已確定，所以AB+BC是固定的，只要DA+CD最小就可以保證送貨路程最短．利用對稱思想，可取點A關於x軸的對稱點A′，連線A′C，交x軸於點D，點D即為所求．
解：略。
圖形及對稱軸
| 名稱 | 對稱軸的條數 | 對稱軸 |
|---|---|---|
角 | 1 | 角平分線所在的直線 |
等腰三角形 | 1 | 底邊上的高（頂角平分線或底邊上的中線）所在的直線 |
等邊三角形 | 3 | 各邊上的高（角平分線或中線）所在的直線 |
等腰梯形 | 1 | 上下底的中線所在的直線 |
菱形 | 2 | 兩條對角線所在的直線 |
圓 | 無數 | 過圓心的每條直線 |
正方形 | 4 | 兩條對角線所在的直線或對邊中線所在的直線 |
半圓 | 1 | 經過圓心且垂直於這個半圓直徑的直線 |
正六邊形 | 6 | 過相對的頂點所在的直線或過對邊中線所在的直線 |
